
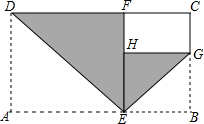
 如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处,则四边形CGHF的周长是( )
如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处,则四边形CGHF的周长是( )| A. | 2a | B. | 2b | C. | 2(a-b) | D. | a+b |
分析 根据矩形性质和折叠得:且根据有三个角是直角的四边形是矩形,证明四边形DAEF是矩形,四边形CFEB是矩形,四边形CFHG是矩形,所以分别求出CF和FH的长,再相加即可周长.
解答 解:由折叠得:DF=AD=b,BE=EH,
∴FC=DC-DF=AB-DF=a-b,
∵四边形ABCD是矩形,
∴∠ADC=∠A=90°,
∵DE平分∠ADC,
∴∠ADE=∠EDC=45°,
∵DC∥AB,
∴∠EDC=∠AED=45°,
由折叠得:∠AED=∠DEF=45°,
∴∠AEF=90°,
∴∠ADC=∠A=∠AEF=90°,
∴四边形DAEF是矩形,
同理四边形CFEB是矩形,四边形CFHG是矩形,
∴BE=FC=a-b,AD=EF=b,
∴EH=BE=a-b,
∴FH=EF-EH=b-(a-b)=2b-a,
∴四边形CGHF的周长是:2FC+2FH=2(a-b)+2(2b-a)=2b;
故选B.
点评 本题主要考查的是翻折的性质、矩形的性质与判定、角平分线,证得四边形CFEB是矩形是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 25.4×10-9 | B. | 2.54×10-10 | C. | 2.54×10-8 | D. | 2.54×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
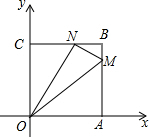 如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=5.
如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com