
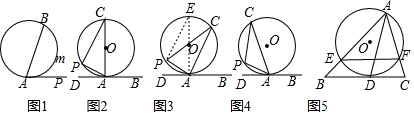
分析 问题1:利用切线的以及圆周角定理即可证明∠PAD=∠PCA;
问题2:首先连接AO并延长交⊙O于点D′,连接PD′,由圆周角定理可得∠D′=∠C,又由AD′是直径,AB切圆于点A,易证得∠PAD=∠PCA,继而证得结论;
运用:连接DF,AD是△ABC中∠BAC的平分线,⊙O与BC切于点D,可得∠FDC=∠EAD,又由圆周角定理可得∠EAD=∠EFD,继而证得结论.
解答 解:问题1:
证明:
∵AC是圆的直径,
∴∠APC=90°,
∴∠ACP+∠PAC=90°,
∵直线DB切⊙O于点A,
∴∠DAC=90°,
∴∠PAD+∠PAC=90°,
∴∠PAD=∠PCA;
问题2:如图4,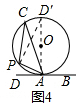
连接AO并延长交⊙O于点D′,连接PD′,
由问题1可知∠PAD=∠D′,
∵∠C=∠D′,
∴∠PAD=∠PCA;
运用:连接DF,如图5,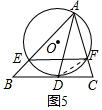
∵AD是△ABC中∠BAC的平分线,
∴∠EAD=∠DAC,
∵⊙O与BC切于点D,
∴∠FDC=∠DAC,
∴∠FDC=∠EAD,
∵在⊙O中∠EAD=∠EFD,
∴∠FDC=∠EFD,
∴EF∥BC.
点评 此题考查了和圆有关的综合性题目,用到的知识点有:切线的性质、圆周角定理以及平行线的判定.注意准确作出辅助线是解此题的关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:填空题
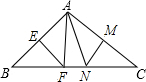 如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.
如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com