
 如图,点G是△ABC的重心,DE过点G且平行于BC,点D、E分别在AB、AC上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$.(用$\overrightarrow{a}$、$\overrightarrow{b}$表示)
如图,点G是△ABC的重心,DE过点G且平行于BC,点D、E分别在AB、AC上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$.(用$\overrightarrow{a}$、$\overrightarrow{b}$表示) 分析 先根据三角形重心的性质(重心到顶点的距离与重心到对边中点的距离之比为2:1),求得$\overrightarrow{DE}$与$\overrightarrow{BC}$的数量关系,然后再根据$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$,可得$\overrightarrow{DE}$与$\overrightarrow{AC}$、$\overrightarrow{AB}$的数量关系.
解答 解:连接AG,并延长AG交BC于点F.
∵DE∥BC,
∴AG:AF=DE:BC;
又∵点G是△ABC的重心,
∴AG:AF=2:3,
∴DE:BC=2:3;即$\overrightarrow{DE}$:$\overrightarrow{BC}$=2:3;
∵$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$,
∴$\overrightarrow{DE}$=$\frac{2}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$,
故答案为:$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$.
点评 本题主要考查了三角形的重心、平面向量.在解答此题时要注意两点:①三角形的重心的性质:重心到顶点的距离与重心到对边中点的距离之比为2:1,即AG:GF=2:1,而不是AG:AF=2:1;②平面向量是有方向的.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:选择题
| A. | a-c>b-c | B. | c-a>c-b | C. | ac>bc | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于( )
如图,直线a∥b,直线l与a相交于点P,与直线b相交于点Q,PM⊥l于点P,若∠1=39°,则∠2等于( )| A. | 61° | B. | 51° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
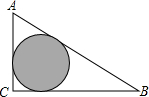 如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com