用铝合金型材做一个形状如图1所示的矩形窗框.设窗框的一边为xm.窗户的透光面积为ym2.y与x的函数图象如图2所示.(图中顶点横坐标为1,纵坐标为1.5)[小题1]⑴写出y与x之间的函数关系式.指出当x为何值时.窗户透光面积最大? [小题2]⑵当窗户透光面积1.125m2时.窗框的两边长各是多少? 题目和参考答案——青夏教育精英家教网—

(本题满分10分)用铝合金型材做一个形状如图1所示的矩形窗框，设窗框的一边为xm，窗户的透光面积为ym²，y与x的函数图象如图2所示.（图中顶点横坐标为1,纵坐标为1.5）

【小题1】⑴写出y与x之间的函数关系式，指出当x为何值时，窗户透光面积最大？
【小题2】⑵当窗户透光面积1.125m²时，窗框的两边长各是多少？

【小题1】解：∵顶点横坐标为1,纵坐标为1.5，
∴y与x之间的函数关系式

……2分
∵抛物线经过点(0，0)
∴a=

,∴y与x之间的函数关系式

……5分
当x=1时，y最大，窗户透光面积最大
【小题2】（2）当窗户透光面积1.125时，y=1.125,
∴

，解得x=

或

……8分
当x=

时，矩形窗框另一边长为

，
当x=

时，矩形窗框另一边长为

∴当窗户透光面积1.125m²，矩形窗框两边长分别为

或

解析:
略

练习册系列答案

名校课堂系列答案

相关习题

科目：初中数学 来源： 题型：

（本题满分10分）下图是小华作的一周的零用钱的统计图（单位：元）

分析上图，请回答下列问题：
（1）周几小华用的零用钱最多，是多少？他零用钱花得最少的一天是多少元？
（2）哪几天他花的零用钱是一样的？分别是多少？
（3）你能帮小华算一算一周平均每天用多少零用钱吗？
（4）估计一下，小华一月用去多少零用钱？（一个月按30天计算）

科目：初中数学 来源：2011-2012学年江苏省兴化市九年级上学期期末四校联考数学卷 题型：解答题

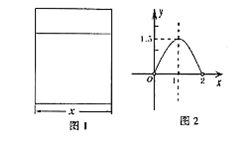
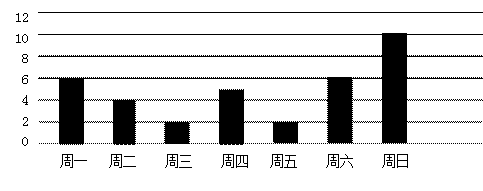
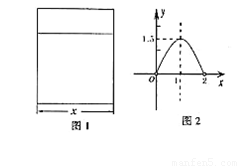
(本题满分10分) 用铝合金型材做一个形状如图1所示的矩形窗框，设窗框的一边为xm，窗户的透光面积为ym²，y与x的函数图象如图2所示.（图中顶点横坐标为1,纵坐标为1.5）

1.⑴写出y与x之间的函数关系式，指出当x为何值时，窗户透光面积最大？

2.⑵当窗户透光面积1.125m²时，窗框的两边长各是多少？

科目：初中数学 来源：2012学年人教版中考数学第一轮复习一元一次方程专项训练 题型：选择题

（2011江苏无锡，28，10分）(本题满分10分)十一届全国人大常委会第二十次会议审议的个人所得税法修正案草案(简称“个税法草案”)，拟将现行个人所得税的起征点由每月2000元提高到3000元，并将9级超额累进税率修改为7级，两种征税方法的1～5级税率情况见下表：