
【题目】已知顶点为A的抛物线y=a(x-![]() )2-2经过点B(-
)2-2经过点B(-![]() ,2),点C(
,2),点C(![]() ,2).
,2).
(1)求抛物线的表达式;
(2)如图1,直线AB与x轴相交于点M,与y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
(3)如图2,点Q是折线A-B-C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN′,若点N′落在x轴上,请直接写出Q点的坐标.

【答案】(1) y=(x-![]() )2-2;(2)△POE的面积为
)2-2;(2)△POE的面积为![]() 或
或![]() ;(3)点Q的坐标为(-
;(3)点Q的坐标为(-![]() ,
,![]() )或(-
)或(-![]() ,2)或(
,2)或(![]() ,2).
,2).
【解析】
(1)将点B坐标代入解析式求得a的值即可得;
(2)由∠OPM=∠MAF知OP∥AF,据此证△OPE∽△FAE得![]() =
=![]()
=![]() =
=![]() ,即OP=
,即OP=![]() FA,设点P(t,-2t-1),列出关于t的方程解之可得;
FA,设点P(t,-2t-1),列出关于t的方程解之可得;
(3)分点Q在AB上运动、点Q在BC上运动且Q在y轴左侧、点Q在BC上运动且点Q在y轴右侧这三种情况分类讨论即可得.
(1)把点B(-![]() ,2)代入y=a(x-
,2)代入y=a(x-![]() )2-2,
)2-2,
解得a=1,
∴抛物线的表达式为y=(x-![]() )2-2,
)2-2,
(2)由y=(x-![]() )2-2知A(
)2-2知A(![]() ,-2),
,-2),
设直线AB表达式为y=kx+b,代入点A,B的坐标得 ,
,
解得![]() ,
,
∴直线AB的表达式为y=-2x-1,
易求E(0,-1),F(0,-![]() ),M(-
),M(-![]() ,0),
,0),
若∠OPM=∠MAF,
∴OP∥AF,
∴△OPE∽△FAE,
∴![]() ,
,
∴OP=![]() FA=
FA=![]()
![]() ,
,
设点P(t,-2t-1),则![]() ,
,
解得t1=-![]() ,t2=-
,t2=-![]() ,
,
由对称性知,当t1=-![]() 时,也满足∠OPM=∠MAF,
时,也满足∠OPM=∠MAF,
∴t1=-![]() ,t2=-
,t2=-![]() 都满足条件,
都满足条件,
∵△POE的面积=![]() OE·|t|,
OE·|t|,
∴△POE的面积为![]() 或
或![]() ;
;
(3)如图,若点Q在AB上运动,过N′作直线RS∥y轴,交QR于点R,交NE的延长线于点S,

设Q(a,-2a-1),则NE=-a,QN=-2a.
由翻折知QN′=QN=-2a,N′E=NE=-a,
由∠QN′E=∠N=90°易知△QRN′∽△N′SE,
∴![]() =
=![]() =
=![]() ,即
,即![]() ==
==![]() =2,
=2,
∴QR=2,ES=![]() ,
,
由NE+ES=NS=QR可得-a+![]() =2,
=2,
解得a=-![]() ,
,
∴Q(-![]() ,
,![]() ),
),
如图,若点Q在BC上运动,且Q在y轴左侧,过N′作直线RS∥y轴,交BC于点R,交NE的延长线于点S.

设NE=a,则N′E=a.
易知RN′=2,SN′=1,QN′=QN=3,
∴QR=![]() ,SE=
,SE=![]() -a.
-a.
在Rt△SEN′中,(![]() -a)2+12=a2,
-a)2+12=a2,
解得a=![]() ,
,
∴Q(-![]() ,2),
,2),
如图,若点Q在BC上运动,且点Q在y轴右侧,过N′作直线RS∥y轴,交BC于点R,交NE的延长线于点S.

设NE=a,则N′E=a.
易知RN′=2,SN′=1,QN′=QN=3,
∴QR=![]() ,SE=
,SE=![]() -a.
-a.
在Rt△SEN′中,(![]() -a)2+12=a2,
-a)2+12=a2,
解得a=![]() ,
,
∴Q(![]() ,2).
,2).
综上,点Q的坐标为(-![]() ,
,![]() )或(-
)或(-![]() ,2)或(
,2)或(![]() ,2).
,2).


科目:初中数学 来源: 题型:
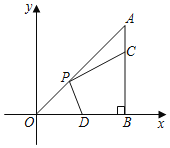
【题目】如图,在Rt△ABO中,∠OBA=90°,A(8,8),点C在边AB上,且![]() ,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )
A.(2,2)B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
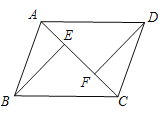
【题目】如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“美丽沧州,清洁乡村”活动中,高家村村长提出了两种购买垃圾桶方案;方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元;设方案1的购买费用和每月垃圾处理费用共为![]() 元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为
元,交费时间为x个月;方案2的购买费和每月垃圾处理费共为![]() 元,交费时间为x个月.
元,交费时间为x个月.
(1)直接写出![]() 、
、![]() 与x的函数关系式;
与x的函数关系式;
(2)在同一坐标系内,画出两个函数的图像;
(3)在垃圾桶使用寿命相同的情况下,哪种方案省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
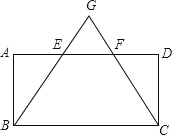
【题目】如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G, GB=GC.
(1)求证:四边形ABCD是矩形;
(2)若△GEF的面积为2.
①求四边形BCFE的面积;
②四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
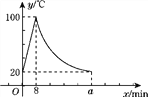
【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“流感”,某学校在休息日用“药熏”消毒法对教室进行消毒.已知药物释放过程中,室内每立方米的含药量y(毫克)与时间x(时)成正比例;药物释放结束后,y与x成反比例;如图所示,根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数解析式;
(2)据测定,当药物释放结束后,每立方米的含药量降至0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多长时间,学生才能进入教室?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com