
【题目】如图,在□ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF.
(1)求证:△AEH≌△CGF;
(2)若EG平分∠HEF,求证:四边形EFGH是菱形.

【答案】(1)答案见解析;(2)答案见解析.
【解析】试题分析:(1)根据全等三角形的判定定理SAS证得结论;
(2)欲证明四边形EFGH是菱形,只需推知四边形EFGH是平行四边形,然后证得该平行四边形的邻边相等即可.
试题解析:证明:(1)∵四边形ABCD是平行四边形,∴∠A=∠C,在△AEH与△CGF中,∵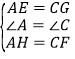 ,∴△AEH≌△CGF(SAS);
,∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,∴AD=BC,AB=CD,∠B=∠D.
∵AE=CG,AH=CF,∴EB=DG,HD=BF,∴△BEF≌△DGH,∴EF=HG.
又∵△AEH≌△CGF,∴EH=GF,∴四边形HEFG为平行四边形,∴EH∥FG,∴∠HEG=∠FGE.∵EG平分∠HEF,∴∠HEG=∠FEG,∴∠FGE=∠FEG,∴EF=GF,∴四边形EFGH是菱形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)平面内将一副三角板按如图1所示摆放,∠EBC= °;
(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α= °;
(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A. 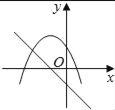 B.
B. 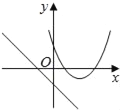 C.
C. 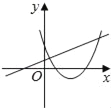 D.
D. 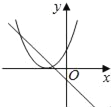
【答案】D
【解析】A.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,与图象不符,故A选项错误;
B.由函数y=mx+m的图象可知m<0,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
<0,则对称轴应在y轴左侧,与图象不符,故B选项错误;
C.由函数y=mx+m的图象可知m>0,即函数y=mx2+2x+2开口方向朝下,与图象不符,故C选项错误;
D.由函数y=mx+m的图象可知m<0,即函数y=mx2+2x+2开口方向朝上,对称轴为x=![]() <0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
<0,则对称轴应在y轴左侧,与图象相符,故D选项正确;
故选:D.
【题型】单选题
【结束】
10
【题目】如图,已知菱形ABCD的周长为16,面积为![]() ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
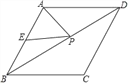
A. 2 B. 2![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=![]() .
.
(1)求证:AMMB=EMMC;
(2)求EM的长;
(3)求sin∠EOB的值.
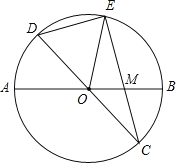
【答案】(1)证明见解析(2)4(3)![]()
【解析】(1)连接A、C,E、B点,那么只需要求出△AMC和△EMB相似,即可求出结论,根据圆周角定理可推出它们的对应角相等,即可得△AMC∽△EMB;
(2)根据圆周角定理,结合勾股定理,可以推出EC的长度,根据已知条件推出AM、BM的长度,然后结合(1)的结论,很容易就可求出EM的长度;
(3)过点E作EF⊥AB,垂足为点F,通过作辅助线,解直角三角形,结合已知条件和(1)(2)所求的值,可推出Rt△EOF各边的长度,根据锐角三角函数的定义,便可求得sin∠EOB的值.
【题型】解答题
【结束】
21
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b;线段AB的中点M表示的数为![]() .
.
[问题情境]
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
![]()
[综合运用]
(1)运动开始前,A、B两点的距离为 ;线段AB的中点M所表示的数 .
(2)点A运动t秒后所在位置的点表示的数为 ;点B运动t秒后所在位置的点表示的数为 ;(用含t的代数式表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(4)若A,B按上述方式继续运动下去,线段AB的中点M能否与原点重合?若能,求出运动时间,并直接写出中点M的运动方向和运动速度;若不能,请说明理由.(当A,B两点重合,则中点M也与A,B两点重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据下列解方程![]() 的过程,请在前面括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为![]() ,
,
去分母,得![]() .(____________________)
.(____________________)
去括号,得![]() .(____________________)
.(____________________)
移项,得![]() .(____________________)
.(____________________)
合并,得![]() .(合并同类项)
.(合并同类项)
(______),得![]() .(______________)
.(______________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,快车到达乙地时,慢车还有( )千米到达甲地.

A. 70 B. 80 C. 90 D. 100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D、E分别是AB、BC边上的中点,过点C作CF∥AB,交DE的延长线于F点,连接CD、BF.
(1)求证:△BDE≌△CFE;
(2)△ABC满足什么条件时,四边形BDCF是矩形?

查看答案和解析>>
科目:初中数学 来源: 题型:
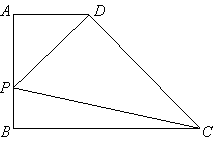
【题目】已知:如图,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上,联结
上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 相交于点
相交于点![]() .设线段
.设线段![]() 的长为
的长为![]() .
.
(1)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)设△![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当△![]() ∽△
∽△![]() 时,求线段
时,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com