
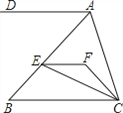
【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
【答案】20°.
【解析】试题分析:先由平行线的性质及∠DAC的度数算出∠ACB的度数,再根据∠ACF的度数求出∠FCB的度数,由CE平分∠BCF得出∠FCE=∠ECB,所以∠ECB的度数就求出来了,再由EF∥AD,AD∥BC,得出EF∥BC(平行公理推论),然后利用平行线性质推出∠FEC=∠ECB,从而得出∠FEC的度数.
试题解析:因为AD∥BC,∠DAC=120°,所以∠ACB=180°-120°=60°(两直线平行,同旁内角互补),又因为∠ACF=20°,所以∠BCF=60°-20°=40°,因为CE平分∠BCF,所以∠ECB=![]() ∠BCF=
∠BCF=![]() ×40°=20°,因为EF∥AD,AD∥BC,所以EF∥BC(根据平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行),所以∠FEC=∠ECB=20°(两直线平行,内错角相等).
×40°=20°,因为EF∥AD,AD∥BC,所以EF∥BC(根据平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行),所以∠FEC=∠ECB=20°(两直线平行,内错角相等).


科目:初中数学 来源: 题型:
【题目】![]() 的几何意义:数轴上表示数a的点与表示数b的点之间的距离。根据
的几何意义:数轴上表示数a的点与表示数b的点之间的距离。根据![]() 的几何意义解答下列问题:
的几何意义解答下列问题:
(1)①![]() 的几何意义是数轴上表示数 的点与 之间的距离。
的几何意义是数轴上表示数 的点与 之间的距离。
②方程![]() ,根据几何意义可解得m的值为 .
,根据几何意义可解得m的值为 .
(2)式子![]() 能取得 值(填“最大”或“最小”),其值为 。
能取得 值(填“最大”或“最小”),其值为 。
(3)已知a,b互为相反数,且![]() ,计算
,计算![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点A,B,C表示的数分别为1,﹣2.5,﹣3观察数轴,与点A的距离为3的点表示的数是 ,B,C两点之间的距离为 ;
(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M ,N ;
(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P ,Q (用含m,n的式子表示这两个数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书200元一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=20 cm,直线AB上有一点C,且BC=6 cm,点M是线段AB的中点,点N是线段BC的中点,则MN=____________ cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com