
| 15 |
| 2 |
 梯形?若存在,求出此刻的t值;若不存在,请说明理由.
梯形?若存在,求出此刻的t值;若不存在,请说明理由.| b |
| 2a |
| 4ac-b2 |
| 4a |
| 15 |
| 2 |
| 15 |
| 2 |
|
|
| 1 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
| BP |
| BD |
| PM |
| CD |
| t |
| 8 |
| PM |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (2011•锦州)如图所示,在边长为1个单位的正方形网格中建立平面直角坐标系,△ABC的顶点均在格点上.
(2011•锦州)如图所示,在边长为1个单位的正方形网格中建立平面直角坐标系,△ABC的顶点均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:
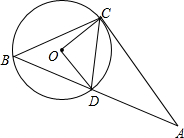 BDO.
BDO.查看答案和解析>>
科目:初中数学 来源: 题型:
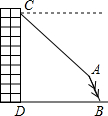 (2011•锦州)如图,小明站在窗口向外望去,发现楼下有一棵倾斜的大树,在窗口C处测得大树顶部A的俯角为45°,若已知∠ABD=60°,CD=20m,BD=16m,请你帮小明计算一下,如果大树倒在地面上,其顶端A与楼底端D的距离是多少米?(结果保留整数,参考数据:
(2011•锦州)如图,小明站在窗口向外望去,发现楼下有一棵倾斜的大树,在窗口C处测得大树顶部A的俯角为45°,若已知∠ABD=60°,CD=20m,BD=16m,请你帮小明计算一下,如果大树倒在地面上,其顶端A与楼底端D的距离是多少米?(结果保留整数,参考数据:| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com