
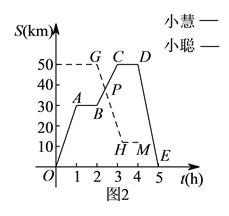
����Ŀ��С�Ϻ�С����ij�羰������ͼ![]() ���ؾ�����·������Լ���ڱ��ݼ��森����
���ؾ�����·������Լ���ڱ��ݼ��森����![]() ��С�۳�������Ϊ
��С�۳�������Ϊ![]() �ĵ綯�����ӱ��ݳ������Ⱥ���������������
�ĵ綯�����ӱ��ݳ������Ⱥ���������������![]() ���Ӻ�
���Ӻ�![]() ���Ӻ�ص����ݣ�С�������г��ӷ��ٳ���������Ϊ
���Ӻ�ص����ݣ�С�������г��ӷ��ٳ���������Ϊ![]() �����Ⱥ�����������������
�����Ⱥ�����������������![]() ���Ӻ�
���Ӻ�![]() ���Ӻ�ص����ݣ�ͼ
���Ӻ�ص����ݣ�ͼ![]() �е�ͼ��ֱ��ʾС�ۺ�С������ݵ�·��
�е�ͼ��ֱ��ʾС�ۺ�С������ݵ�·��![]() ��ʱ��
��ʱ��![]() �ĺ�����ϵ����ȫ�����Խ��ͼ����Ϣ�ش�
�ĺ�����ϵ����ȫ�����Խ��ͼ����Ϣ�ش�
��![]() ��С�������ľ�����__________����
��С�������ľ�����__________����![]() ������Ϊ__________��
������Ϊ__________��
��![]() ����С�Ϻ�С������ʱ�������Ǿ�����ݶ���ǧ�ף�
����С�Ϻ�С������ʱ�������Ǿ�����ݶ���ǧ�ף�

���𰸡���![]() ���ݵ�ͷ�����
���ݵ�ͷ����� ![]() ����
����![]() ��С����С�۵�һ����������
��С����С�۵�һ����������![]() ���ڶ�����������
���ڶ�����������![]() ��
��
�������������������1���۲�ͼ1��ͼ2���з������ɵã�
��2������ME���۲�ͼ���֪�����������������ֱ������⼴��.
����������������ݵ� �� ���٣� ![]() ��
��
�١�С�۵�һ��ͣ�����ھ����![]() �����ڶ���ͣ�����ھ����
�����ڶ���ͣ�����ھ����![]() ����
����
�߲֡ݵ�������![]() �����پ����
�����پ����![]() ��
��
��С�������˲ݵ�ͷ��٣�
��С���ڲݵ�������![]() ���ӣ�
���ӣ�
��![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() �������꼴Ϊ�ݵ����ݵľ��룻
�������꼴Ϊ�ݵ����ݵľ��룻
��2��С���ڷ���������![]() ���ӣ���
���ӣ���![]() ������ΪС�ϵ����־����
������ΪС�ϵ����־����![]() �����ij���Ϊ
�����ij���Ϊ![]() ��
��
��С�ϵ����¸�����ʱ����![]() ��Сʱ��
��Сʱ��
��![]() ��
��
�֡�С������������![]() ���ӣ�
���ӣ�
��![]() ��
��
ͬ����С�ϵ�������ǣ�����![]() Сʱ��
Сʱ��
��С����С��ͬʱ������ݣ���ȫͼ�й�ϵ������![]() ����ͼ�пɿ���С����С������������
����ͼ�пɿ���С����С������������
��![]() ��
�� ![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��С����С�۵�һ����������![]() ���ڶ�����������
���ڶ�����������![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������������һ����ABC����Ҫ�����������ͼ��ֻ�ܽ���������
��1��������ABC��BC���ϵĸ�AD��
��2�������Ƚ���ABC����ƽ��6��������ƽ��3������A1B1C1��
��3����һ����BCP��Ҫ��������ڸ������P����A���غϣ���ʹ�����������ABC����������ش��������������ĵ�P��________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A(2��0)��B(0��4)������BOC��ʹ��BOC����ABOȫ�ȣ����C����Ϊ________________________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ�� ����C�ڡ�O�ϣ�����O��![]() ��BC�ڵ�E������O�ڵ�D��CD��AB.
��BC�ڵ�E������O�ڵ�D��CD��AB.
(1)��֤��EΪOD���е㣻
(2)��CB=6�����ı���CAOD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� P �� m + 3 �� m + 1 ���� x ���ϣ��� P ������Ϊ( )
A.�� 0 ���� 2 ��B.�� 0 ���� 4 ��C.�� 4 �� 0 ��D.�� 2 �� 0 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1����b2������b��2������b3��
��2����x��y��3����y��2��2����y��2��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
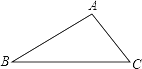
����Ŀ����֪����ͼ������ABC�У���B=30������C=45����AC=2![]() ��
��
����1��AB�ij�Ϊ________��
��2��S��ABC=________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���P��AB��һ���㣨����A��B�غϣ����Խ���AC��BD�ཻ�ڵ�O������P�ֱ���AC��BD�Ĵ��ߣ��ֱ�AC��BD�ڵ�E��F����AD��BC�ڵ�M��N�����н��ۣ��١�APE�ա�AME����PM+PN=AC����PE2+PF2=PO2���ܡ�POF�ס�BNF��������PMN�ס�AMPʱ����P��AB���е㣮������ȷ�Ľ��۵ĸ����У���������.

A.5 B.4 C.3 D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���뽫����֤�����̲���������
��֪����ͼ����P��CD�ϣ���֪��BAP+��APD=180������1=��2
��֤����E=��F

֤��������BAP+��APD=180������֪��
�� �� �� ��
���BAP= �� ��
���ߡ�1=��2����֪��
���BAP�� = ����2
����3= ����ʽ�����ʣ�
��AE��PF�� ��
���E=��F�� ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com