
 如图,在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
如图,在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
分析 先由图形翻折变换的性质得出AE=A′E,再根据A′为CE的中点可知AE=A′E=$\frac{1}{2}$CE,故AE=$\frac{1}{3}$AC,$\frac{AE}{CE}$=$\frac{1}{3}$,再由∠C=90°,DE⊥AC可知DE∥BC,故可得出△ADE∽△ABC,由相似三角形的性质可知$\frac{DE}{BC}=\frac{AE}{BC}=\frac{1}{3}$,故可得出结论.
解答 解:∵△A′DE△ADE翻折而成,
∴AE=A′E,
∵A′为CE的中点,
∴AE=A′E=$\frac{1}{2}$CE,
∴AE=$\frac{1}{3}$AC,$\frac{AE}{CE}$=$\frac{1}{3}$,
∵∠C=90°,DE⊥AC,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AE}{BC}$=$\frac{1}{3}$,
∴$\frac{DE}{6}=\frac{1}{3}$,
解得DE=2.
故选:B.
点评 本题考查的是图形的翻折变换及相似三角形的判定与性质,熟知图形翻折不变性的性质是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
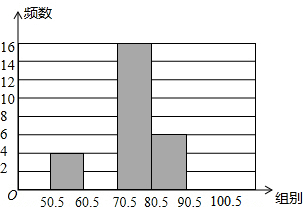 青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随机抽取了部分学生的成绩 (得分取正整数,满分为100分) 作为样本,绘制成如下尚未完成的频数分布表和频数分布直方图.
青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随机抽取了部分学生的成绩 (得分取正整数,满分为100分) 作为样本,绘制成如下尚未完成的频数分布表和频数分布直方图.| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 14 | 0.28 |
| 70.5~80.5 | 16 | a |
| 80.5~90.5 | b | c |
| 90.5~100.5 | 10 | 0.2 |
| 合计 | d | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com