
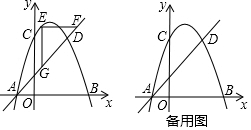
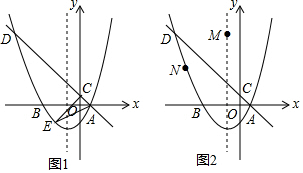
 如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C,M为抛物线的顶点.
如图,二次函数y=x2+bx+c的图象经过A(-1,0)和B(3,0)两点,且交y轴于点C,M为抛物线的顶点.分析 (1)将点A和点B的坐标代入抛物线的解析式求得b、c的值即可;
(2)先求得抛物线的顶点M的坐标,然后再求得点C的坐标,接下来,再求得直线CB的解析式,将x=1代入直线BC的解析式求得对应的y值为-2,由平移后的抛物线的顶点坐标在△△BOC的内部,可得到-2<-4+m<0,最后解不等组即可;
(3)当点P在Q的上时,由平行四边形的性质可知点P的纵坐标为3,当点P在点Q的下方时,由平行四边形的性质可知点P的纵坐标为-3,然后分别将y=3和y=-3代入抛物线的解析式求得对应的x的值即可.
解答 解:(1)将点A和点B的坐标代入得:$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得:b=-2,c=-3.
∴抛物线的解析式为y=x2-2x-3.
(2)∵y=x2-2x-3=(x-1)2-4,
∴M(1,-4).
把x=0代入抛物线的解析式得:y=-3,
∴C(0,-3).
设直线BC的解析式为y=kx+b,则$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$,解得:k=1,b=-3.
∴直线BC的解析式为y=x-3.
把x=1代入y=x-3得:y=-2,
∵平移后的抛物线的顶点坐标在△△BOC的内部,
∴-2<-4+m<0,解得2<m<4.
(3)当点P在Q的上时,由平行四边形的性质可知点P的纵坐标为3.
把y=3代入抛物的解析式x2-2x-3=3,解得:x=1+$\sqrt{7}$或x=1-$\sqrt{7}$.
∴点P的坐标为(1+$\sqrt{7}$,3)或(1-$\sqrt{7}$,3).
当点P在点Q的下方时,由平行四边形的性质可知点P的纵坐标为-3.
把y=-3代入抛物的解析式x2-2x-3=-3,解得:x=2或x=0(舍去)
∴点P的坐标为(2,-3).
综上所述,当点P的坐标为(1-$\sqrt{7}$,3)或(1+$\sqrt{7}$,3)或(2,-3)时,以点B,C,P,Q为顶点的四边形是平行四边形.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、平行四边形的性质,依据平移后的抛物线的顶点坐标在△△BOC的内部列出关于m的不等式是解答问题(2)的关键,依据平行四边形的性质求得P的纵坐标是解答问题(3)的关键.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
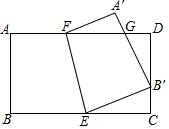 如图,矩形ABCD中,AD=5,E、F分别是BC、AD边上的点,AF=x,四边形ABEF沿EF翻折至A′B′EF,点B′恰好落在边CD上,A′B′与AD相交于点G,△B′GD≌△FGA′.
如图,矩形ABCD中,AD=5,E、F分别是BC、AD边上的点,AF=x,四边形ABEF沿EF翻折至A′B′EF,点B′恰好落在边CD上,A′B′与AD相交于点G,△B′GD≌△FGA′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
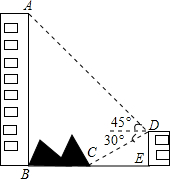 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=100m,DE=20m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=100m,DE=20m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
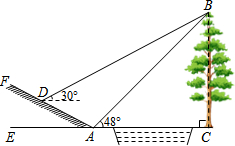 如图所示,某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$取1.73.
如图所示,某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:$\sqrt{3}$,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,$\sqrt{3}$取1.73.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
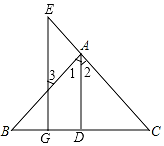 看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.
看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,求证:AD平分∠BAC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com