
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=9,BD=2.
![]()
(1)求AC的长;
(2)若点E在直线AD上,且EA=1,求BE的长.
【答案】(1)5;(2)BE的长为8或6
【解析】
(1)由中点的定义可得CD=2BD,由BD=2可求CD的长度,最后根据线段的和差即可解答;
(2)由于点E在直线AD上位置不确定,需分E在线段DA上和线段AD的延长线两种情况解答.
解:(1)∵点B为CD的中点,BD=2,
∴CD=2BD=4,
∵AD=9,
∴AC=AD﹣CD=9﹣4=5;
(2)若E在线段DA的延长线,如图1,
![]()
∵EA=1,AD=9,
∴ED=EA+AD=1+9=10,
∵BD=2,
∴BE=ED﹣BD=10﹣2=8,
若E线段AD上,如图2,

EA=1,AD=9,
∴ED=AD﹣EA=,9﹣1=8,
∵BD=2,
∴BE=ED﹣BD=8﹣2=6,
综上所述,BE的长为8或6.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(1,﹣3),将△ABC向右平移5个单位长度,再向上平移3个单位长度得到△![]() ,其中点
,其中点 ![]() 分别是点A,B,C的对应点.
分别是点A,B,C的对应点.
(1)请你在给出的坐标系中画出![]() 和写出点A′,C′的坐标;
和写出点A′,C′的坐标;
(2)若△ABC内的一点P经过上述平移后的对应点为![]() ,用含
,用含![]() 的式子表示P点的坐标 ;(直接写出结果即可)
的式子表示P点的坐标 ;(直接写出结果即可)
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为_____;
(3)△ACD为 三角形,四边形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明将一张正方形卡纸剪去一个宽为4cm的长方形(记作A)后,再将剩下的长方形卡纸剪去一个宽为5cm的长方形(记作B).

(1)若长方形A与B的面积均为Scm2,求S的值.
(2)若A的周长是B的周长的![]() 倍,求原正方形的边长.
倍,求原正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A,B,C,D,E对应的数分别为a,b,c,d,e,
![]()
(1)化简:|a﹣c|﹣2|b﹣a|﹣|b﹣c|;
(2)若这五个点满足每相邻两个点之间的距离都相等,且|a|=|e|,|b|=3,直接写出b﹣e的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15,那么△ACD的面积为( )

A. 15 B. 10 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节小长假”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
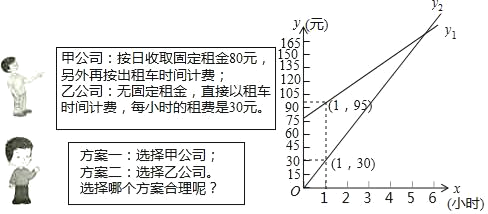
根据以上信息,解答下列问题:
(1)甲公司每小时的租费是 元;
(2)设租车时间为x小时,租用甲公司的车所需费用为y1元,租用乙公司的车所需费用为y2元,分别求出y1,y2关于x的函数解析式;
(3)请你帮助小明计算并分析选择哪个出游方案合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com