
分析 ①②利用三角形内角和定理求得各个角的度数进行判断;
③④⑤利用勾股定理的逆定理即可判断.
解答 解:①∵∠A-∠B=∠C,
∴∠A=∠B+∠C,
∴∠A=90°,
∴△ABC是直角三角形;
②设∠A=3x°,则∠B=4x°,∠C=5x°,
∵∠A+∠B+∠C=180°,
∴3x+4x+5x=180,
∴x=15,
∴∠A=45°,则∠B=60°,∠C=75°,
∴△ABC不是直角三角形;
③∵b2=a2-c2,
∴b2+c2=a2,
∴此三角形是直角三角形,故③正确.
④∵a:b:c=1:3:2,
∴设a=x,则b=3x,c=2c,
∴a+c=b,则不能构成三角形,故④错误;
⑤a2+b2=(m2-n2)+(2mn)2=m4+n2+2m2n2,
c2=(m2+n2)2=m4+n4+2m2n2,
∴a2+b2=c2.
则△ABC是直角三角形,故⑤正确.
故答案是:①③⑤.
点评 本题考查了三角形的内角和定理和勾股定理的逆定理,正确利用完全平方公式的变形证明⑤是本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (a2+1+2a)(a2+1-2a) | B. | (a2-2a+1)2 | C. | (a-1)4 | D. | (a+1)2(a-1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
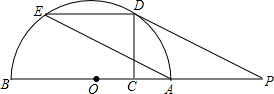 如图,AB为半圆O的直径,点C是OA的中点,CD⊥OA交半圆O于点D,点E是$\widehat{BD}$的中点,过点D作DP∥AE交BA的延长线于点P.求证:
如图,AB为半圆O的直径,点C是OA的中点,CD⊥OA交半圆O于点D,点E是$\widehat{BD}$的中点,过点D作DP∥AE交BA的延长线于点P.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com