
 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2$\sqrt{2}$,P是AC上的一个动点.
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2$\sqrt{2}$,P是AC上的一个动点.分析 (1)根据30°的直角三角形和等腰直角三角形的性质求出各边的长,再将两三角形面积相加即为四边形ABCD的面积;
(2)分两种情况:如图2和图3,利用三角函数的特殊值求出∠PDF的度数,再根据图形位置求出∠PDA的度数;
(3)如图4,根据(1)中结论可知,DP=CP=$\frac{{\sqrt{6}}}{2}$,再利用平行线的距离相等可知:PC就是□DPBQ的边PD所对应的高,代入面积公式求出面积即可.
解答 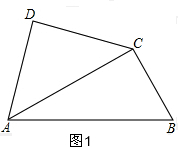 解:(1)如图1,在Rt△ABC中,∵∠CAB=30°,AB=2$\sqrt{2}$,
解:(1)如图1,在Rt△ABC中,∵∠CAB=30°,AB=2$\sqrt{2}$,
∴BC=$\frac{1}{2}$AB=$\sqrt{2}$,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{(2\sqrt{2})^{2}-(\sqrt{2})^{2}}$=$\sqrt{6}$,
∵△ACD是等腰直角三角形,
∴AD=$\frac{AC}{\sqrt{2}}$=$\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{3}$,
∴S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{6}$+$\frac{1}{2}$×$\sqrt{3}$×$\sqrt{3}$=$\frac{3}{2}$+$\sqrt{3}$,
故答案为:$\sqrt{3}$,$\sqrt{6}$,$\sqrt{2}$,$\frac{3}{2}+\sqrt{3}$;
(2)当P点位置如图2所示时,
根据(1)中结论,DF=$\frac{{\sqrt{6}}}{2}$,∠ADF=45°,
又∵PD=BC=$\sqrt{2}$,
∴cos∠PDF=$\frac{DF}{PD}$=$\frac{\sqrt{3}}{2}$,
∴∠PDF=30°,
∴∠PDA=∠ADF-∠PDF=15°;
当P点位置如图3所示时,同(2)可得∠PDF=30°,
∴∠PDA=∠ADF+∠PDF=75°;
∴此时∠PDA的度数为15°或75°;
(3)如图4,
在□DPBQ中,BC∥DP,
∵∠ACB=90°,
∴DP⊥AC
根据(1)中结论可知,DP=CP=$\frac{{\sqrt{6}}}{2}$,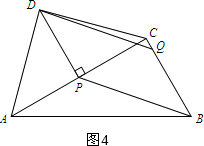
∴S□DPBQ=DP•CP=$\frac{\sqrt{6}}{2}$×$\frac{\sqrt{6}}{2}$=$\frac{3}{2}$.
则当点P运动到距离点C为$\frac{\sqrt{6}}{2}$时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上,此时?DPBQ的面积为$\frac{3}{2}$.
点评 本题是四边形的综合题,考查了一副三角板所形成的四边形的边和角的关系;根据动点P的运动路线确定其所形成的边和角的关系,利用三角函数和勾股定理求边和角的大小,得出结论.


科目:初中数学 来源: 题型:解答题
 取一张长与宽之比为5:2的长方形纸板,剪去四个边长为5cm的小正方形(如图),并用它做一个无盖的长方体形状的包装盒,要使包装盒的容积为200cm3(纸板的厚度略去不计),问:这张长方形纸板的长与宽分别为多少厘米?
取一张长与宽之比为5:2的长方形纸板,剪去四个边长为5cm的小正方形(如图),并用它做一个无盖的长方体形状的包装盒,要使包装盒的容积为200cm3(纸板的厚度略去不计),问:这张长方形纸板的长与宽分别为多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{-a}$ | B. | $\sqrt{-a}$ | C. | -$\sqrt{a}$ | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1≥y2 | C. | y1<y2 | D. | y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,分别以线段AB的两个端点A、B为圆心,以5cm长为半径画弧,两弧相交于点C、D,连结AC、BC、AD、BD,得到四边形ADBC.若AB=6cm,则四边形ADBC的面积为24cm2.
如图,分别以线段AB的两个端点A、B为圆心,以5cm长为半径画弧,两弧相交于点C、D,连结AC、BC、AD、BD,得到四边形ADBC.若AB=6cm,则四边形ADBC的面积为24cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com