
����Ŀ���Ķ����в��ϣ���������������⣺
���ǿ��Խ�������λ����ʾΪ![]() ������a��b��c�ֱ��ʾ��λ�ϵ����֣�ʮλ�ϵ����ֺ�λ�ϵ����֣���a ��0������Ȼ
������a��b��c�ֱ��ʾ��λ�ϵ����֣�ʮλ�ϵ����ֺ�λ�ϵ����֣���a ��0������Ȼ![]() =100a +10b +c����������
=100a +10b +c����������![]() ��
��![]() ��������λ����Ϊһ�����������������x��y��z��������������Ȼ�����磺123��321��һ���������678��876��һ�������������
��������λ����Ϊһ�����������������x��y��z��������������Ȼ�����磺123��321��һ���������678��876��һ�������������
��1����������������������
��2��һ�ԡ���������ĺ�Ϊ1110������ԡ����������
��3�������x��ʾ��λ���֣���֤������һ������������ĺ��ܱ�37������
���𰸡���1��234��432��һ���������345��543��һ���������
��2����ԡ��������λ654��456.
��3����������
��������
��1��������������������弴��ֱ��д�����������������
��2������������������������һ����λ������ʾ�������������������ͣ���1110����������⼴�ɣ�
��2����ʾ����������������������ͣ�д��37��6��x1�����ж�6��x1�����������ɣ�
��1�������������������������ã�234��432��һ���������345��543��һ���������
��2�����������������е�һ����λ����ʮλ����Ϊx����λ����Ϊ��x1������λ����Ϊ��x��1������xΪ����1С��9����������
�������λ��Ϊ100��x��1����10x��x1��111x��99��
����һ����λ����ʮλ����Ϊx����λ����Ϊ��x��1������λ����Ϊ��x1�����������λ��Ϊ100��x1����10x��x��1��111x99��
���������������ĺ�Ϊ��111x��99������111x99����222x��1110��
��x��5���������⣬
����ԡ��������λ654��456.
��3����x��ʾһ����λ���İ�λ���֣���xΪ����2С��9����������
�������������������ã������λ����ʮλ����Ϊ��x1������λ����Ϊ��x2����
����������100x��10��x1������x2����111x12��
�����������������100��x2����10��x1����x��111x210��
���������������ĺ�Ϊ����111x12������111x210����222x222��222��x1����37��6��x1����
��xΪ����2С��9��������
�ࣨx1����������
��6��x1����������
��37��6��x1���ܱ�37������
��������һ������������ĺ��ܱ�37������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E�ǶԽ���BD��һ�㣨�����B��D�غϣ�������E��EF��AB����EF=AB������AE��BF��CF��
��1����DE=DC����֤���ı���CDEF�����Σ�
��2����AB=![]() ��BC=3�����ı���ABFE�ܳ���Сʱ���ı���CDEF���ܳ�Ϊ__________��
��BC=3�����ı���ABFE�ܳ���Сʱ���ı���CDEF���ܳ�Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�OΪԭ�㣬ABCD�ı�AB��x���ϣ���D��y���ϣ���A������Ϊ����2��0����AB=6����BAD=60������E��BC����һ�㣬CE=3EB����P��A��O��D���㣬������y=ax2+bx+c����A��B��D���㣮
��1���������ߵĽ���ʽ��
��2����֤��DE�ǡ�P�����ߣ�
��3��������CDE�Ƶ�D˳ʱ����ת90������E�Ķ�Ӧ��E��������������y=ax2+bx+c������˵�����ɣ�
��4������MΪ�������ߵĶ��㣬ƽ�����Ƿ���ڵ�N��ʹ���Ե�B��D��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ij����ʻ�����У������е�ʣ������y����������ʻ·��x��ǧ�ף�֮����һ�κ�����ϵ���䲿��ͼ����ͼ��ʾ��
��1����y����x�ĺ�����ϵʽ��
��2����֪�������е�ʣ������Ϊ8��ʱ���������Ὺʼ��ʾ���ͣ��ڴ˴���ʻ�����У���ʻ��450ǧ��ʱ��˾��������ǰ������ļ���վ��75ǧ��·�̣��ڿ����ü���վ��;�У���������ʼ��ʾ����ʱ�������վ��·���Ƕ���ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֪ʶ��
�����dz�����ѧ��һ����Ҫ���ߣ�����������Խ������������Ľ�ϣ��о��������Ƿ�����������Ҫ�Ĺ��ɣ�������A�㡢B���ʾ����Ϊa��b����A��B����֮��ľ���AB=|a-b|����a��b����ɼ�ΪAB=a-b���߶�AB���е�M��ʾ����Ϊ![]() ��
��
�������龳��
��֪��������A��B���㣬�ֱ��ʾ����Ϊ-10��8����A��ÿ��3����λ���ٶ����������������˶�����B��ÿ��2����λ���������˶������˶�ʱ��Ϊt�루t��0����
![]()
���ۺ����ã�
��1���˶���ʼǰ��A��B����ľ���Ϊ______���߶�AB���е�M����ʾ����______��
��2����A�˶�t�������λ�õĵ��ʾ����Ϊ______����B�˶�t�������λ�õĵ��ʾ����Ϊ______�����ú�t��ʽ�ӱ�ʾ��
��3�����ǰ�������ʽ�˶���A��B���㾭�������������������������ʾ������ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O���ң�OB=2����B=30����C����AB������һ�㣨�����A��B�غϣ�������CO���ӳ�CO����O�ڵ�D������AD��
��1��AB=_____��
��2������D=20��ʱ�����BOD�Ķ�����
��3������ACD����BCO���ƣ���AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1����24��11015
��2����3������![]() ����
����![]()
��3������![]() ����
����![]()
��4��1�£���1��+0��4��5��0.1������2��3
��5������1��2009+����2��3+2������3��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
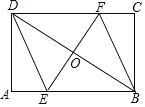
����Ŀ����ͼ������ABCD�У�AB=6��BC=4�����Խ���BD�е�O��ֱ�߷ֱ�AB��CD���ڵ�E��F��
��1����֤���ı���BEDF��ƽ���ı��Σ�
��2�����ı���BEDF������ʱ����EF�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com