Question

20．如图，在Rt△ABC中，∠ABC=90°，∠CAB=45°，MN为AB的垂直平分线，E为MN上一点，连接AE，过点E作AE⊥EF，过点B作AC的平行线BF．
（1）求证：AE=EF；
（2）连接CE，若∠ECA=30°，DH=1，求BF的长．

Answer 1

分析 （1）如图1，连接BE，设∠EAC=α，分别求出∠EBF和∠F的度数，相等，则EB=AF，再由垂直平分线的性质得AE=EB，所以AE=AF；
（2）如图2，作辅助线，构建全等三角形和直角三角形，先证明△AEI≌△EBJ，得EI=BJ，由30°角所对直角边是斜边的一半和等腰三角形三线合一的性质得EC=BF，最后求出EC的长，就是BF的长．

解答 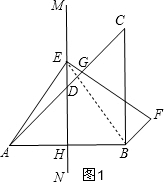证明：（1）如图1，连接BE，设∠EAC=α，
∵AE⊥EF，
∴∠AEG=90°，
∴∠EAC+∠EGA=90°，
∴∠EGA=90°-α，
∵AC∥BF，
∴∠F=∠EGA=90°-α，∠CBF=∠C=45°，
∵MN是AB的垂直平分线，
∴AE=EB，∠EAB=∠EBA，
∴∠EBF=90°+45°-∠EBA=135°-∠EAB=135°-（45°+α）=90°-α，
∴∠F=∠EBF，
∴EB=AF，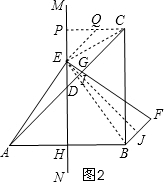
∴AE=AF；
（2）过E作EJ⊥BF于J，交AC于I，垂足为I，
∵EB=EF，
∴∠BEJ=∠JEF，
∵∠EAC+∠AEI=90°，∠JEF+∠AEI=90°，
∴∠EAC=∠JEF=∠BEJ，
∵∠AIE=∠BJE=90，
∵AE=BE，
∴△AEI≌△EBJ，
∴EI=BJ=$\frac{1}{2}$BF，
在Rt△EIC中，∠=30°，
∴EI=$\frac{1}{2}$EC，
∴EC=BF，
过C作CP⊥MN于P，则CP=BH=DH=1，
∴∠PCE=45°-30°=15°，
作∠QEC=∠PCE=15°，交PC于Q，则QE=QC，
∴∠EQP=30°，
设EP=x，则EQ=QC=2x，PQ=$\sqrt{3}$x，
则PC=PQ+QC，
∴1=2x+$\sqrt{3}$x，
x=2-$\sqrt{3}$，
∵EC²=PE²+PC²，
则EC²=（2-$\sqrt{3}$）²+[（2+$\sqrt{3}$）（2-$\sqrt{3}$）]²，
∴EC=$\sqrt{6}$-$\sqrt{2}$，
∴BF=EC=$\sqrt{6}$-$\sqrt{2}$．

点评 本题是三角形的综合题，考查了直角三角形30°角、等腰直角三角形、平行线、线段垂直平分线的性质；做好本题的关键是恰当地构建辅助线，利用三角形全等及等腰三角形三线合一的性质得出边与角的关系，利用等量代换求出结论．