
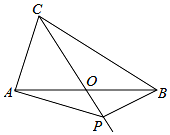
 如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$.
如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$. 分析 分是最清楚讨论即可:①如图1中,当点P在CO的延长线上,∠APB=90°时.②如图2中,当点P在线段CO上,∠APB=90°时.③如图3中,当∠ABP=90°时.分别解直角三角形即可.
解答 解:①如图1中,当点P在CO的延长线上,∠APB=90°时,作PE⊥AB于E.
∵∠AOC=∠POE=45°,∠PEO=90°
∴OE=PE,
∵OA=OB,∠APB=90°,
∴OP=$\frac{1}{2}$AB=3,
∴OE=PE=$\frac{3\sqrt{2}}{2}$,
在Rt△AEP中,AP=$\sqrt{A{E}^{2}+P{E}^{2}}$=$\sqrt{(\frac{3\sqrt{2}}{2})^{2}+(3+\frac{3\sqrt{2}}{2})^{2}}$=$\sqrt{18+9\sqrt{2}}$.
②如图2中,当点P在线段CO上,∠APB=90°时,作PE⊥AB于E.
∵∠AOC=∠POE=45°,∠PEO=90°
∴OE=PE,
∵OA=OB,∠APB=90°,
∴OP=$\frac{1}{2}$AB=3,
∴OE=PE=$\frac{3\sqrt{2}}{2}$,
在Rt△AEP中,AP=$\sqrt{A{E}^{2}+P{E}^{2}}$=$\sqrt{(3-\frac{3\sqrt{2}}{2})^{2}+(\frac{3\sqrt{2}}{2})^{2}}$=$\sqrt{18-9\sqrt{2}}$.
③如图3中,当∠ABP=90°时,
∵∠BOP=∠AOC=45°,∠OBP=90°,
∴OP=PB=3,
在Rt△ABP中,AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
综上所述,当△PAB为直角三角形时,AP的长$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$.
点评 本题考查等腰三角形的性质、等腰直角三角形的性质、勾股定理、解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,注意不能漏解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
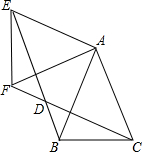 如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D查看答案和解析>>
科目:初中数学 来源: 题型:解答题
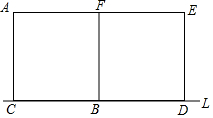 如图,已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF,且CB与BD均在直线L上,将正方形ACBF沿直线L以1单位/秒向右平移,设移动时间为t秒,正方形ACBF在移动过程中与正方形BDEF重叠的面积为S,试求:
如图,已知边长等于8个单位长度的两个完全相同的正方形ACBF、BDEF有公共边BF,且CB与BD均在直线L上,将正方形ACBF沿直线L以1单位/秒向右平移,设移动时间为t秒,正方形ACBF在移动过程中与正方形BDEF重叠的面积为S,试求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 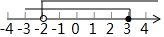 | ||
| C. | 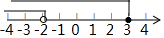 | D. | 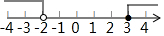 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com