
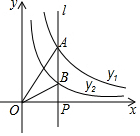
 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2的值等于( )
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1-k2的值等于( )| A. | 1 | B. | 3 | C. | 6 | D. | 8 |
分析 根据反比例函数k的几何意义可知:△AOP的面积为$\frac{{k}_{1}}{2}$,△BOP的面积为$\frac{{k}_{2}}{2}$,由题意可知△AOB的面积为$\frac{{k}_{1}}{2}$-$\frac{{k}_{2}}{2}$=3,依此可求k1-k2的值.
解答 解:根据反比例函数k的几何意义可知:△AOP的面积为$\frac{{k}_{1}}{2}$,△BOP的面积为$\frac{{k}_{2}}{2}$,
∴△AOB的面积为$\frac{{k}_{1}}{2}$-$\frac{{k}_{2}}{2}$,
∴$\frac{{k}_{1}}{2}$-$\frac{{k}_{2}}{2}$=3,
∴k1-k2=6.
故选C.
点评 本题考查反比例函数k的几何意义,解题的关键是正确理解k的几何意义,本题属于中等题型.


科目:初中数学 来源: 题型:解答题
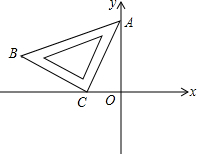 如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限.
如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,∠ACB=90°,AC=BC,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
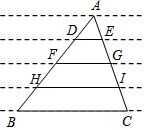 如图一组平行线,每相邻两条平行线间的距离都相等,△ABC的三个顶点都在平行线上,则图中一定等于$\frac{1}{4}$BC的线段是DE.
如图一组平行线,每相邻两条平行线间的距离都相等,△ABC的三个顶点都在平行线上,则图中一定等于$\frac{1}{4}$BC的线段是DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
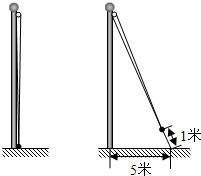 为了测算出学校旗杆的高度,爱动脑筋的小明这样设计出了一个方案如图,将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现此时绳子底端距离打结处约1米,则旗杆的高度是12米.
为了测算出学校旗杆的高度,爱动脑筋的小明这样设计出了一个方案如图,将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现此时绳子底端距离打结处约1米,则旗杆的高度是12米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
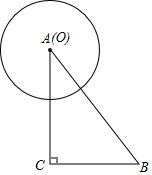 如图,Rt△ABC中,∠C=90°,AC=4cm,BC=3m,以点O为圆心,2m长度为半径的⊙O以1cm/s的速度从点A出发,沿着边AB-BC-CA运动,当圆心O回到点A时停止运动,设运动时间为ts.
如图,Rt△ABC中,∠C=90°,AC=4cm,BC=3m,以点O为圆心,2m长度为半径的⊙O以1cm/s的速度从点A出发,沿着边AB-BC-CA运动,当圆心O回到点A时停止运动,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
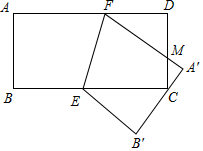 如图,已知在矩形ABCD中,AB=13.AD=27,将它沿EF折叠,恰好使得点C落在边A′B′上(点A的对应点位A′,点B的对应点为B′),且把线段A′B′分成4:9两部分(A′C<B′C),A′F与CD相交于点M,则折痕EF的长度为$\frac{13}{3}$$\sqrt{10}$.
如图,已知在矩形ABCD中,AB=13.AD=27,将它沿EF折叠,恰好使得点C落在边A′B′上(点A的对应点位A′,点B的对应点为B′),且把线段A′B′分成4:9两部分(A′C<B′C),A′F与CD相交于点M,则折痕EF的长度为$\frac{13}{3}$$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
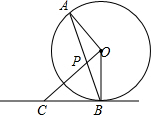 如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB.
如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com