
【题目】如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.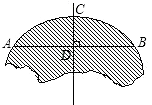
(1)求作此残片所在的圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
【答案】
(1)解:作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
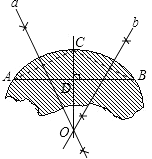
(2)解:连接OA,
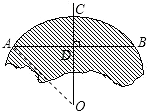
设OA=x,AD=12cm,OD=(x﹣8)cm,
则根据勾股定理列方程:
x2=122+(x﹣8)2,
解得:x=13.
答:圆的半径为13cm.
【解析】(1)根据垂径定理作图即可。作出AB的垂直平分线,再作出AC的垂直平分线即可。
(2)连接OA,在Rt△AOD中,根据勾股定理列方程求解即可。
【考点精析】根据题目的已知条件,利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各抽取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:

(1)这三个厂家的广告,分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传?
(2)如果三个厂家产品的售价一样,作为顾客的你选购哪个厂家的产品?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )

A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
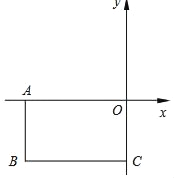
【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
(2)如图,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置.
(1)在直角坐标系中,画出平移后所得△A′B′C′(其中B′、C′分别是B、C的对应点);
(2)求△ABC的面积;
(3)以A、B、C、D为顶点构造平行四边形,则D点坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.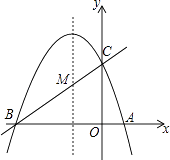
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com