
【题目】(2016广西省贺州市第25题)如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
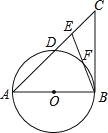
【答案】(1)、证明过程见解析;(2)、1.6
【解析】
试题分析:(1)、由AE=AB,可得∠ABE=90°﹣![]() ∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;(2)、首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;(2)、首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)、∵AE=AB, ∴△ABE是等腰三角形,
∴∠ABE=![]() (180°﹣∠BAC=)=90°﹣
(180°﹣∠BAC=)=90°﹣![]() ∠BAC, ∵∠BAC=2∠CBE, ∴∠CBE=
∠BAC, ∵∠BAC=2∠CBE, ∴∠CBE=![]() ∠BAC,
∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣![]() ∠BAC)+
∠BAC)+![]() ∠BAC=90°, 即AB⊥BC, ∴BC是⊙O的切线;
∠BAC=90°, 即AB⊥BC, ∴BC是⊙O的切线;
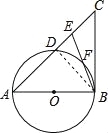
(2)、连接BD,∵AB是⊙O的直径, ∴∠ADB=90°, ∵∠ABC=90°, ∴∠ADB=∠ABC,
∵∠A=∠A, ∴△ABD∽△ACB, ∴![]() =
=![]() , ∵在Rt△ABC中,AB=8,BC=6, ∴AC=
, ∵在Rt△ABC中,AB=8,BC=6, ∴AC=![]() =10,
=10,
∴![]() , 解得:AD=6.4, ∵AE=AB=8, ∴DE=AE﹣AD=8﹣6.4=1.6.
, 解得:AD=6.4, ∵AE=AB=8, ∴DE=AE﹣AD=8﹣6.4=1.6.


科目:初中数学 来源: 题型:
【题目】下图是由一些火柴棒搭成的图案:
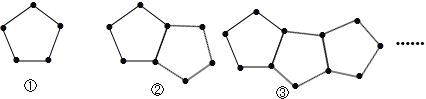
(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
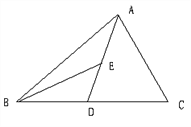
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司年前缴税20万元,今年缴税24.2万元.若该公司这两年的年均增长率相同,设这个增长率为x,则列方程( )
A.20(1+x)3=24.2
B.20(1﹣x)2=24.2
C.20+20(1+x)2=24.2
D.20(1+x)2=24.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016四川省乐山市第16题)在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若![]() ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.
例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数![]() 图象上点M的“可控变点”,则点M的坐标为 ;
图象上点M的“可控变点”,则点M的坐标为 ;
(2)若点P在函数![]() (
(![]() )的图象上,其“可控变点”Q的纵坐标y′的取值范围是
)的图象上,其“可控变点”Q的纵坐标y′的取值范围是![]() ,则实数a的取值范围是 .
,则实数a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com