
分析 (1)设小张加工1件A型零件需要x小时,加工1件B型零件需要y小时,根据题意列出方程组,求出方程组的解即可得到结果;
(2)表示出小张每月加工的零件件数,进而列出W与a的函数,利用一次函数性质确定出最大值,即可作出判断.
解答 解:(1)设小张加工1件A型零件需要x小时,加工1件B型零件需要y小时,
根据题意得:$\left\{\begin{array}{l}{x+3y=5}\\{2x+5y=9}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
则小张加工1件A型零件需要2小时,加工1件B型零件需要1小时;
(2)由(1)可得小张每月加工A型零件a件时,还可以加工B型零件(8×25-2a)件,
根据题意得:W=16a+12×(8×25-2a)+800=-8a+3200,
∵-8<0,
∴W随a的增大而减小,
当a=50时,W最大值为2800,
∵2800<3000,
∴该公司执行后违背了在工资待遇方面的承诺.
点评 此题考查了一次函数的应用,以及二元一次方程组的应用,弄清题中的数量关系是解本题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:选择题
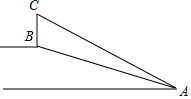 某风景区在坡度为7:24的斜坡AB上有一座标志性建筑物BC.在点A处测得建筑物顶部C的仰角为31°.斜坡AB的长度为100米.则这座建筑物BC的高度约为( )(结果精确到0.1米,参考数据:sin31°≈0.52,tan31°≈0.60)
某风景区在坡度为7:24的斜坡AB上有一座标志性建筑物BC.在点A处测得建筑物顶部C的仰角为31°.斜坡AB的长度为100米.则这座建筑物BC的高度约为( )(结果精确到0.1米,参考数据:sin31°≈0.52,tan31°≈0.60)| A. | 21.9米 | B. | 29.6米 | C. | 35.0米 | D. | 57.6米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
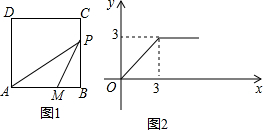 如图1,四边形ABCD是正方形,M是边AB上一点,AM=2cm,动点P从点B出发,以每秒acm的速度沿BC-CD-DA运动到点A停止,△AMP的面积y(cm2)与动点P的运动时间x(秒)的关系如图2(部分)所示.
如图1,四边形ABCD是正方形,M是边AB上一点,AM=2cm,动点P从点B出发,以每秒acm的速度沿BC-CD-DA运动到点A停止,△AMP的面积y(cm2)与动点P的运动时间x(秒)的关系如图2(部分)所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
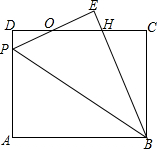 如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com