
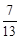 千米,到达对岸AD最少要用 小时。
千米,到达对岸AD最少要用 小时。

 =5km,
=5km, ×AC×CD=30km2,
×AC×CD=30km2, km,
km, km/小时,
km/小时, 小时=0.4小时.
小时=0.4小时.

科目:初中数学 来源:不详 题型:解答题
 在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序:
在几何学中,通常用点表示位置,用线段的长度表示两点间的距离,用一条射线表示一个方向。在线段的两个端点中(如图),如果我们规定一个顺序: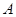 为始点,
为始点,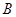 为终点,我们就说线段
为终点,我们就说线段 具有射线的
具有射线的 方向,线段
方向,线段 叫做有向线段,记作
叫做有向线段,记作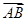 ,线段
,线段 的长度叫做有向线段
的长度叫做有向线段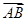 的长度(或模),记作
的长度(或模),记作 。
。
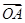 (有向线段与
(有向线段与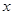 轴的长度单位相同),
轴的长度单位相同), ,
,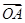 与
与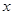 轴的正半轴的夹角是
轴的正半轴的夹角是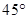 ,且与
,且与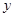 轴的正半轴的夹角是
轴的正半轴的夹角是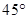 ;
;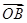 的终点
的终点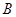 的坐标为(3,
的坐标为(3, ),求它的模及它与
),求它的模及它与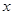 轴的正半轴的夹角
轴的正半轴的夹角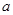 的度数。
的度数。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
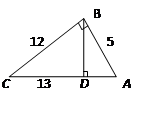 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
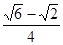 ,cosl5°=
,cosl5°=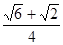 )
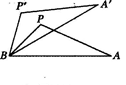
) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com