
【题目】在平面直角坐标系![]() 中,存在抛物线
中,存在抛物线![]() 以及两点
以及两点![]() 和
和![]() .
.
(1)求该抛物线的顶点坐标;
(2)若该抛物线经过点![]() ,求此抛物线的表达式;
,求此抛物线的表达式;
(3)若该抛物线与线段![]() 只有一个公共点,结合图象,求
只有一个公共点,结合图象,求![]() 的取值范围.
的取值范围.
【答案】(1)(0,2);(2)![]() ;(3)m=2或
;(3)m=2或![]() .
.
【解析】
(1)![]() 是顶点式,可得到结论;
是顶点式,可得到结论;
(2)把A点坐标代入![]() 得方程,于是得到结论;
得方程,于是得到结论;
(3)分两种情况:当抛物线开口向上或向下时,分别画出图形,找到临界位置关系,求出m的值,再进行分析变化趋势可得到结论.
(1)![]() 是顶点式,顶点坐标为
是顶点式,顶点坐标为![]() ;
;
(2)∵抛物线经过点![]() ,
,
∴m=9m +2,
解得: ![]() ,
,
∴![]()
(3)如图1,当抛物线开口向上时,抛物线顶点在线段![]() 上时,
上时,![]() ;
;
当m>2时,直线x=1交抛物线于点(1,m+2),交点位于点B上方,所以此时线段![]() 与抛物线一定有两个交点,不符合题意;
与抛物线一定有两个交点,不符合题意;
如图2,当抛物线开口向下时,抛物线顶过点![]() 时,
时,![]() ;
;
直线x=-3交抛物线于点(-3,9m+2),当![]() 时,9m+2<m,交点位于点A下方,直线x=1交抛物线于点(1,m+2),交点位于点B上方,所以此时线段
时,9m+2<m,交点位于点A下方,直线x=1交抛物线于点(1,m+2),交点位于点B上方,所以此时线段![]() 与抛物线一定有且只有一个交点,符合题意;
与抛物线一定有且只有一个交点,符合题意;
综上所述,当![]() 或
或![]() 时,抛物线与线段
时,抛物线与线段![]() 只有一个公共点.
只有一个公共点.




 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
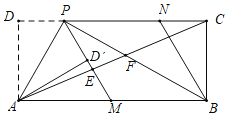
【题目】在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD'P,PD'的延长线交边AB于点M,过点B作BN∥MP交DC于点N,连接AC,分别交PM,PB于点E,F.现有以下结论:
①连接DD',则AP垂直平分DD';
②四边形PMBN是菱形;
③AD2=DPPC;
④若AD=2DP,则![]() ;
;
其中正确的结论是_____(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,其中图象与
的部分图象如图所示,其中图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() .
.

![]() 求此二次函数的解析式;
求此二次函数的解析式;
![]() 将此二次函数的解析式写成
将此二次函数的解析式写成![]() 的形式,并直接写出顶点坐标以及它与
的形式,并直接写出顶点坐标以及它与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标.
的坐标.
![]() 利用以上信息解答下列问题:若关于
利用以上信息解答下列问题:若关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 为实数)在
为实数)在![]() 的范围内有解,则
的范围内有解,则![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:下图是华师版九年级上册数学教材第77页的部分内容.
猜想
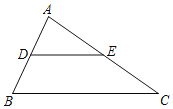
如图,在△ABC中,点D、E分别是AB与AC的中点,根据画出的图形,可以猜想:
DE∥BC,且DE=![]() BC.
BC.
对此,我们可以用演绎推理给出证明
证明在△ABC中,
∵点D、E分别是AB与AC的中点,
∴![]() 请根据教材提示,结合图①,写出完整证明过程,
请根据教材提示,结合图①,写出完整证明过程,
结论应用:
如图②在四边形ABCD中,AD=BC,点P是对角线BD的中点,M是DC中点,N是AB中点,MN与BD相交于点Q.
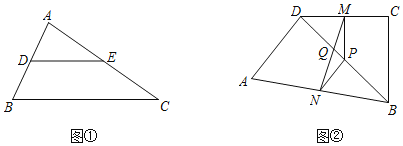
(1)求证:∠PMN=∠PNM;
(2)若AD=BC=4,∠ADB=90°,∠DBC=30°,则PQ= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,y是关于
,y是关于![]() 的二次函数,抛物线
的二次函数,抛物线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 抛物线
抛物线![]() 经过点
经过点![]() 则下列判断:
则下列判断:

①四条抛物线的开口方向均向下;
②当![]() 时,四条抛物线表达式中的
时,四条抛物线表达式中的![]() 均随
均随![]() 的增大而增大;
的增大而增大;
③抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 顶点的上方;
顶点的上方;
④抛物线![]() 与
与![]() 轴交点在点
轴交点在点![]() 的上方.
的上方.
其中正确的是
A.①②④B.①③④
C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC=____________度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A、B(点A在点B的左侧),且AB=6.
轴交于点A、B(点A在点B的左侧),且AB=6.
(1)求这条抛物线的对称轴及表达式;
(2)在y轴上取点E(0,2),点F为第一象限内抛物线上一点,联结BF、EF,如果![]() ,求点F的坐标;
,求点F的坐标;
(3)在第(2)小题的条件下,点F在抛物线对称轴右侧,点P在![]() 轴上且在点B左侧,如果直线PF与y轴的夹角等于∠EBF,求点P的坐标.
轴上且在点B左侧,如果直线PF与y轴的夹角等于∠EBF,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习函数的过程中,我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程,根据你所经历的学习过程,现在来解决下面的问题:在函数y=ax3﹣bx+2中,当x=﹣1时,y=4;当x=﹣2时 y=0.
(1)根据已知条件可知这个函数的表达式 .
(2)根据已描出的部分点,画出该函数图象.
(3)观察所画图象,回答下列问题:
①该图象关于点 成中心对称;
②当x取何值时,y随着x的增大而减小;
③若直线y=c与该图象有3个交点,直接写出c的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,试探索线段BC,DC,EC之间满足的等量关系,并证明你的结论.

(2)如图②,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC边上,试探索线段AD,BD,CD之间满足的等量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com