
【题目】重庆育才中学需要为老校友们订制![]() 周年纪念吉祥物“陶娃”,原计划订
周年纪念吉祥物“陶娃”,原计划订![]() 份,每份
份,每份![]() 元,订制公司表示:如果多订,可以优惠.根据校庆当天前来的校友数量,学校最终订了
元,订制公司表示:如果多订,可以优惠.根据校庆当天前来的校友数量,学校最终订了![]() 份,并按原价八折购买,但订制公司获得了同样的利润.
份,并按原价八折购买,但订制公司获得了同样的利润.
(1)求订制公司生产每套“陶娃”的成本;
(2)求订制公司获得的利润.
科目:初中数学 来源: 题型:
【题目】“万州古红桔”原名“万县红桔”,古称丹桔(以下简称为红桔),种植距今至少已有一千多年的历史,“玫瑰香橙”(源自意大利西西里岛塔罗科血橙,以下简称香橙)现已是万州柑橘发展的主推品种之一.某水果店老板在2017年11月份用15200元购进了400千克红桔和600千克香橙,已知香橙的每千克进价比红桔的每千克进价2倍还多4元.
(1)求11月份这两种水果的进价分别为每千克多少元?
(2)时下正值柑橘销售旺季,水果店老板决定在12月份继续购进这两种水果,但进入12月份,由于柑橘的大量上市,红桔和香橙的进价都有大幅下滑,红桔每千克的进价在11月份的基础上下降了![]() m%,香橙每千克的进价在11月份的基础上下降了m%,由于红桔和“玫瑰香橙”都深受库区人民欢迎,实际水果店老板在12月份购进的红桔数量比11月份增加了
m%,香橙每千克的进价在11月份的基础上下降了m%,由于红桔和“玫瑰香橙”都深受库区人民欢迎,实际水果店老板在12月份购进的红桔数量比11月份增加了![]() m%,香橙购进的数量比11月份增加了2m%,结果12月份所购进的这两种柑橘的总价与11月份所购进的这两种柑橘的总价相同,求m的值.
m%,香橙购进的数量比11月份增加了2m%,结果12月份所购进的这两种柑橘的总价与11月份所购进的这两种柑橘的总价相同,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道:如果点A.B在数轴上分别表示有理数a、b,那么A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|ab|.
根据上述材料,利用数轴解答下列问题:
![]()
(1)如果点A在数轴上表示2,将点A先向左平移2个单位长度,再向右移动7个单位长度,那么终点B在数轴上表示的数是___;
(2)数轴上表示x和1的两个点之间的距离是___;
(3)若|x3|+|x+2|=7,则x的值是___;
(4)在(1)的条件下,设点P在数轴上表示的数为x,当|PA||PB|=2时,则x的值是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店正在开展“感恩十年,童行有你”促销活动一次性购物不超过![]() 元不享受优惠;一次性购物超过
元不享受优惠;一次性购物超过![]() 元但不超过
元但不超过![]() 元,超过
元,超过![]() 元的部分九折优惠;一次性购物超过
元的部分九折优惠;一次性购物超过![]() 元一律八折.在活动期间,张三两次购物分别付款
元一律八折.在活动期间,张三两次购物分别付款![]() 元、
元、![]() 元,若张三选择这两次购物合并成一次性付款可以节省___________元.
元,若张三选择这两次购物合并成一次性付款可以节省___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为2,
的边长为2, ![]() 边在
边在![]() 轴上,
轴上, ![]() 的中点与原点
的中点与原点![]() 重合,过定点
重合,过定点![]() 与动点
与动点![]() 的直线
的直线![]() 记作
记作![]() .
.

(1)若![]() 的解析式为
的解析式为![]() ,判断此时点
,判断此时点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(2)当直线![]() 与
与![]() 边有公共点时,求
边有公共点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣![]() x+
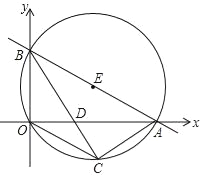
x+![]() 分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
分别与x轴、y轴交于A、B两点,⊙E经过原点O及A、B两点,C是⊙E上一点,连接BC交OA于点D,∠COD=∠CBO.
(1)求A、B、C三点坐标;
(2)求经过O、C、A三点的抛物线解析式;
(3)直线AB上是否存在点P,使得△COP的周长最小?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市第八中学校为给学生营造良好舒适的休息环境,决定改造校园内的—小花园,如图是该花园的平面示意图,它是由![]() 个正方形拼成的长方形用以种植六种不同的植物,已知中间最小的正方形
个正方形拼成的长方形用以种植六种不同的植物,已知中间最小的正方形![]() 的边长是
的边长是![]() 米,正方形
米,正方形![]() 、
、![]() 边长相等.请根据图形特点求出该花园的总面积.
边长相等.请根据图形特点求出该花园的总面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
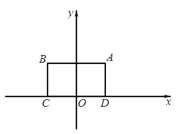
【题目】对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为(![]() ,
,![]() ),顶点C、D在x轴上,且OC=OD.
),顶点C、D在x轴上,且OC=OD.
(1)当⊙P的半径为4时,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成为矩形ABCD的“等距圆”的圆心的是 ;
)中可以成为矩形ABCD的“等距圆”的圆心的是 ;
②如果点P在直线![]() 上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
上,且⊙P是矩形ABCD的“等距圆”,求点P的坐标;
(2)已知点P在![]() 轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
轴上,且⊙P是矩形ABCD的“等距圆”,如果⊙P与直线AD没有公共点,直接写出点P的纵坐标m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com