
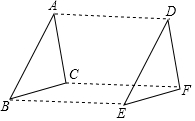
 如图,△DEF是由△ABC平移得到的,对于结论:①BC=EF;②AB∥DE;③△ABC≌△DEF;④四边形ACFD为平行四边形,正确的是( )
如图,△DEF是由△ABC平移得到的,对于结论:①BC=EF;②AB∥DE;③△ABC≌△DEF;④四边形ACFD为平行四边形,正确的是( )| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ②③④ |
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=$\frac{3}{4}$,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或$\frac{7}{2}$;④0<BE≤5,其中正确的结论是①③(填入正确结论的序号)
如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=$\frac{3}{4}$,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或$\frac{7}{2}$;④0<BE≤5,其中正确的结论是①③(填入正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 解分式必定产生增根 | |
| B. | 若分式方程的根是零,则必定是增根 | |
| C. | 解分式方程必须验根 | |
| D. | x=3是方程$\frac{x}{x-3}$=2+$\frac{3}{x-3}$的根 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 百分位 | B. | 个位 | C. | 千位 | D. | 十万位 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{60}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 系数是-$\frac{1}{2}$,次数是4 | B. | 系数是-$\frac{1}{2}$,次数是3 | ||
| C. | 系数是-2,次数是4 | D. | 系数是-2,次数是3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com