
分析 (1)设这时水面高x厘米,根据放进一个棱长为20cm的正方形铁块后,铁块的顶面仍然高于水面,根据水的体积没变,可列出方程,然后求解即可;
(2)设这时水面高y厘米,根据放进一个棱长为10cm的正方形铁块后,铁块浸没在水中,根据水的体积没变,可列方程解决问题.
解答 解:(1)设这时水面高x厘米,根据题意得:
(50×40-20×20)x=50×40×10,
解得:x=12.5,
答:这时水面高12.5厘米;
(2)设这时水面高y厘米,根据题意得:
50×40y=50×40×20+10×10×10,
解得:y=20.5,
答:这时水面高20.5厘米.
点评 此题考查了一元一次方程的应用,读懂题意,根据前后水的体积不变列出方程是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
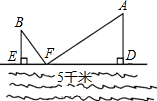 如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.
如图,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路AD,BE,AD=3千米,BE=2千米,且两条小路之间的距离为5千米.现要在江边建一个供水站F向A,B两厂送水,若供水管路最短,则EF=2千米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x-y}{{{x^2}+{y^2}}}$ | B. | $\frac{xy-y}{3xy}$ | C. | $\frac{m-1}{1-m}$ | D. | $-\frac{61m}{32m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
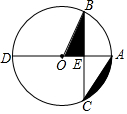 如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )
如图,在☉O中,直径AD交弦BC于E,OE=AE,∠ACB=30°,BC=4,则图中阴影部分的面积为( )| A. | $\frac{8}{9}π-\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{8}{9}π-\frac{{4\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{18}π-\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{16}{9}π-\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.
我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
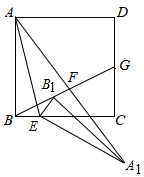 如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com