
【题目】关于![]() 的方程
的方程![]() 的整数解(
的整数解(![]() )的组数为( ).
)的组数为( ).
A. 2组B. 3组C. 4组D. 无穷多组
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】若一个矩形的一边是另一边的两倍,则称这个矩形为方形.如图1,矩形![]() 中,
中,![]() ,则称
,则称![]() 为方形.
为方形.

(Ⅰ)设![]() 是方形的一组邻边,写出
是方形的一组邻边,写出![]() 的一组值为__________;
的一组值为__________;
(Ⅱ)在![]() 中,将
中,将![]() 分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使得这些矩形的边
分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使得这些矩形的边![]() 的对边分别在
的对边分别在![]() 上,如图2所示.
上,如图2所示.
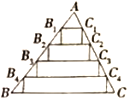
①若![]() ,
,![]() 边上的高为
边上的高为![]() ,判断以
,判断以![]() 为一边的矩形是否是方形?_________(填“是”或“否”);②若以
为一边的矩形是否是方形?_________(填“是”或“否”);②若以![]() 为一边的矩形为方形,则
为一边的矩形为方形,则![]() 与
与![]() 边上的高之比为__________.
边上的高之比为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
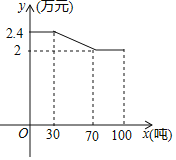
【题目】某县积极响应市政府加大产业扶贫力度的号召,决定成立草莓产销合作社,负责扶贫对象户种植草莓的技术指导和统一销售,所获利润年底分红.经市场调研发现,草莓销售单价![]() (万元)与产量x(吨)之间的关系如图所示
(万元)与产量x(吨)之间的关系如图所示![]() .已知草莓的产销投入总成本
.已知草莓的产销投入总成本![]() (万元)与产量x
(万元)与产量x![]() (吨)之间满足
(吨)之间满足![]() .
.
(1)直接写出草莓销售单价![]() (万元)与产量
(万元)与产量![]() (吨)之间的函数关系式;
(吨)之间的函数关系式;
(2)求该合作社所获利润![]() (万元)与产量
(万元)与产量![]() (吨)之间的函数关系式;
(吨)之间的函数关系式;
(3)为提高农民种植草莓的积极性,合作社决定按![]() 万元/吨的标准奖励扶贫对象种植户,为确保合作社所获利润
万元/吨的标准奖励扶贫对象种植户,为确保合作社所获利润![]() (万元)不低于
(万元)不低于![]() 万元,产量至少要达到多少吨?
万元,产量至少要达到多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一种适用于笔记本电脑的铝合金支架,边![]() ,
,![]() 可绕点
可绕点![]() 开合,在
开合,在![]() 边上有一固定点
边上有一固定点![]() ,支柱
,支柱![]() 可绕点
可绕点![]() 转动,边
转动,边![]() 上有六个卡孔,其中离点
上有六个卡孔,其中离点![]() 最近的卡孔为
最近的卡孔为![]() ,离点
,离点![]() 最远的卡孔为
最远的卡孔为![]() .当支柱端点
.当支柱端点![]() 放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得
放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得![]() 的长为
的长为![]() ,
,![]() 为
为![]() ,支柱
,支柱![]() 为
为![]() .
.

(1)当支柱的端点![]() 放在卡孔
放在卡孔![]() 处时,求
处时,求![]() 的度数;
的度数;
(2)当支柱的端点![]() 放在卡孔
放在卡孔![]() 处时,
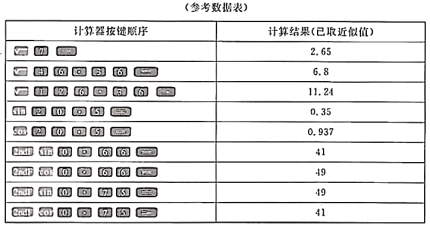
处时,![]() ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
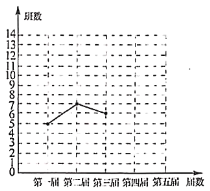
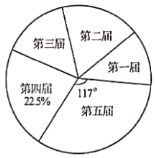
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知双曲线![]() 与直线
与直线![]() 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线![]() 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线![]() 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1x2<0,|x1|+|x2|=4,点A,C在直线y2=-3x+t上.
(1)求点C的坐标;
(2)当y1随着x的增大而增大时,求自变量x的取值范围;
(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2-5n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
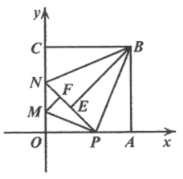
【题目】如图,在平面直角坐标系![]() 第一象限中有正方形
第一象限中有正方形![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上一动点
轴上一动点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折后,点
翻折后,点![]() 落在点
落在点![]() 处。在
处。在![]() 上有一点
上有一点![]() ,使得将
,使得将![]() 沿直线
沿直线![]() 翻折后,点
翻折后,点![]() 落在直线
落在直线![]() 上的点
上的点![]() 处,直线
处,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
I.求证:![]() ;
;
Ⅱ.求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
Ⅲ.当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (b,c为常数).
(b,c为常数).
(1)若抛物线的顶点坐标为(1,1),求b,c的值;
(2)若抛物线上始终存在不重合的两点关于原点对称,求c的取值范围;
(3)在(1)的条件下,存在正实数m,n( m<n),当m≤x≤n时,恰好有![]() ,求m,n的值.
,求m,n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com