
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,将
上,将![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,且
处,且![]() .
.
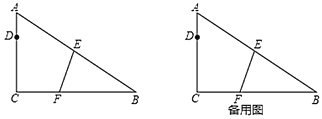
(1)求![]() 的长;
的长;
(2)点![]() 是射线
是射线![]() 上的一个动点,连接
上的一个动点,连接![]() ,
,![]() ,
,![]() ,
,![]() 的面积与
的面积与![]() 的面积相等,
的面积相等,
①当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的长;
的长;
②当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ________;
________;
(3)将直线![]() 平移,平移后的直线与直线
平移,平移后的直线与直线![]() ,直线
,直线![]() 分别交于点
分别交于点![]() 和点
和点![]() ,以线段
,以线段![]() 为一边作正方形
为一边作正方形![]() ,点
,点![]() 与点
与点![]() 在直线
在直线![]() 两侧,连接
两侧,连接![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)如图1中,连接DF,在Rt△DCF中,利用勾股定理,构建方程即可解决问题.
(2)①如图2-1中,当DG∥BC时,S△DGC=S△DGB.设BG=x.利用平行线分线段成比例定理即可解决问题.
②如图2-2中,当点G在BA的延长线上时,证明AB=2AG时,满足条件.
(3)如图3中,当PD∥BC时,作QK⊥BC于K.利用全等三角形以及相似三角形的性质解决问题即可.
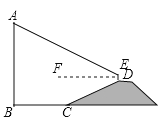
解:(1)如图1中,连接DF,
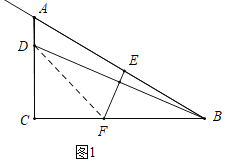
∵将△ABC沿直线EF折叠,点B恰好落在AC边上的点D处
∴DF=BF
在Rt△DCF中,DF2=DC2+CF2,
∴(6-CF)2=9+CF2,
∴CF=![]() .
.
(2)①如图2-1中,当DG∥BC时,S△DGC=S△DGB.设BG=x.

在Rt△ACB中,AC=4,BC=6,
∴AB=![]() ,
,
∵DG∥BC,
∴![]() ,
,
∴![]() ,
,
∴x=![]() .
.
②如图2-2中,当点G在BA的延长线上时,
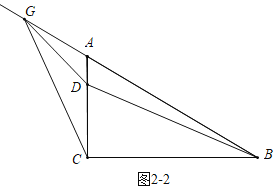
∵CD=3AD,
∴S△GDC=3S△GAD,
∴当S△ADB=2S△ADG时,S△GDC=S△GBD,
∴AB=2AG,
∴AG=![]() ,
,
∴GB=3![]() .
.
综上:GB=![]() 或
或![]() ;
;
(3)如图3中,当PD∥BC时,作QK⊥BC于K.

∵四边形MNPQ是正方形,
∴易证△PDN≌△NCM≌△MKA,
∴KQ=CM=DN,KM=CN=PD,
∵△PDN∽△BCD,
∴![]() ,
,
∴![]() ,
,
∴PD=2DN,
∴CN=2DN,
∴DN=1,CN=2,
∴KQ=DN=CM=1,KM=CN=2,
∴BK=9,
∴tan∠QBC=![]() .
.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 均为的等边三角形,点
均为的等边三角形,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 与
与![]() 平行的直线交射线
平行的直线交射线![]() 于点
于点![]() .
.
(1)当![]() ,
,![]() ,
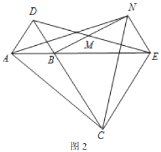
,![]() 三点在同一直线上时(如图1),求证:
三点在同一直线上时(如图1),求证:![]() 为
为![]() 中点;
中点;
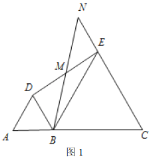
(2)将图1中的![]() 绕点
绕点![]() 旋转,当
旋转,当![]() ,
,![]() ,
,![]() 三点在同一直线上时(如图2),求证:
三点在同一直线上时(如图2),求证:![]() 为等边三角形;
为等边三角形;
(3)将图2中![]() 绕点
绕点![]() 继续顺时针旋转多少度时,点
继续顺时针旋转多少度时,点![]() 恰好第一次位于线段
恰好第一次位于线段![]() 中点,试作出图形并直接写出
中点,试作出图形并直接写出![]() 绕点
绕点![]() 继续旋转的度数.
继续旋转的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y = ax2 2ax + c图像的顶点为P,与x轴交于A、B两点(其中点A在点B的左侧),与y轴交于点C,它的对称轴交直线BC交于点D,且CD︰BD=1︰2.
(1)求B点坐标;
(2)当△CDP的面积是1时,求二次函数的表达式;
(3)若直线BP交y轴于点E,求当△CPE是直角三角形时的a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点M是![]() 轴正半轴上任意一点,过点M作PQ∥
轴正半轴上任意一点,过点M作PQ∥![]() 轴,分别交函数
轴,分别交函数![]() 和
和![]() 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )

A.∠POQ不可能等于90°B.![]()
C.这两个函数的图象一定关于![]() 轴对称D.△POQ的面积是
轴对称D.△POQ的面积是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
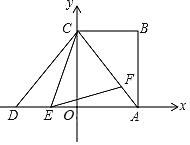
【题目】如图,矩形ABCD的顶点A、C在平面直角坐标系的坐标轴上,AB=4,CB=3,点D与点A关于y轴对称,点E、F分别是线段DA、AC上的动点(点E不与A、D重合),且∠CEF=∠ACB,若△EFC为等腰三角形,则点E的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,BC=CD,连接AC、BD,∠ADB=90°.
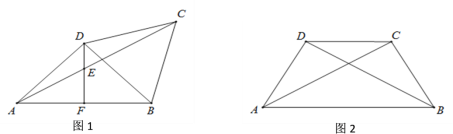
(1)如图1,若AD=BD=BC,过点D作DF⊥AB于点F,交AC于点E:
①∠DAC= °;
②求证:EC=EA+ED;
(2)如图2,若AC=BD,求∠DAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是垂直于水平面的建筑物,为测量
是垂直于水平面的建筑物,为测量![]() 的高度,小红从建筑物底端
的高度,小红从建筑物底端![]() 出发,沿水平方向行走了52米到达点
出发,沿水平方向行走了52米到达点![]() ,然后沿斜坡
,然后沿斜坡![]() 前进,到达坡顶
前进,到达坡顶![]() 点处,
点处,![]() .在点
.在点![]() 处放置测角仪,测角仪支架
处放置测角仪,测角仪支架![]() 高度为0.8米,在
高度为0.8米,在![]() 点处测得建筑物顶端
点处测得建筑物顶端![]() 点的仰角
点的仰角![]() 为
为![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),斜坡
在同一平面内),斜坡![]() 的坡度(或坡比)
的坡度(或坡比)![]() ,求建筑物
,求建筑物![]() 的高度.(精确到个位)(参考数据:
的高度.(精确到个位)(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
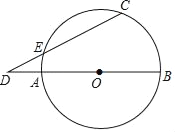
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,点D在BA的延长线上,CD与⊙O交于另一点E,DE=OB=2,∠D=20°,则弧BC的长度为( )
A. ![]() π B.
π B. ![]() π C.
π C. ![]() π D.
π D. ![]() π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com