
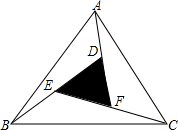
 如图所示是一块三角形纸板,其中AD=DF,BE=ED,EF=FC,一只蚂蚁在这张纸上爬行,求蚂蚁踩到阴影部分的概率.
如图所示是一块三角形纸板,其中AD=DF,BE=ED,EF=FC,一只蚂蚁在这张纸上爬行,求蚂蚁踩到阴影部分的概率. 分析 利用等底同高的三角形面积相等的概念,将△ABC分为7个面积相同的三角形,中间阴影部分的三角形的面积是△ABC的$\frac{1}{7}$,所以蚂蚁踩到阴影部分的概率是$\frac{1}{7}$.
解答  解:连接AE,BF,CD,
解:连接AE,BF,CD,
∵AD=DF,BE=ED,EF=FC,利用三角形中线的性质可得,
∴S△ADC=S△CDF,S△AED=S△ABE,S△BEF=S△EFD,S△EBF=S△BFC,S△ABD=S△BDF,S△AEF=S△AFC,
∴△ABC被分为7个面积相同的三角形,中间阴影部分的三角形的面积是△ABC的$\frac{1}{7}$,
所以蚂蚁踩到阴影部分的概率是$\frac{1}{7}$.
点评 此题主要考查了三角形中线的性质以及几何概率等知识,利用三角形中线的性质得出面积相等的三角形是解题关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
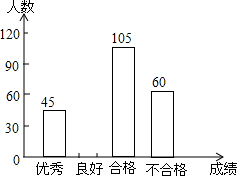 为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:
为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
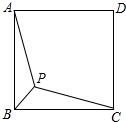 如图,点P是正方形ABCD内一点,连接AP、BP、CP,若BP=$\sqrt{3}$,CP=$\sqrt{30}$,∠BPA=135°,则正方形ABCD的边长为$\sqrt{39}$.
如图,点P是正方形ABCD内一点,连接AP、BP、CP,若BP=$\sqrt{3}$,CP=$\sqrt{30}$,∠BPA=135°,则正方形ABCD的边长为$\sqrt{39}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
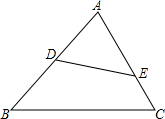 如图,已知D、E分别在△ABC的边AB、AC上,D为AB的中点,AE:EC=2:1,△ADE∽△ACB,且∠ADE=∠C,求$\frac{DE}{BC}$的值.
如图,已知D、E分别在△ABC的边AB、AC上,D为AB的中点,AE:EC=2:1,△ADE∽△ACB,且∠ADE=∠C,求$\frac{DE}{BC}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com