
分析 (1)根据已知条件得到A(6,0),B(0,3),求得OA=6,OB=3,根据三角函数的定义即可得到结论;
(2)将点A向左平移12个单位到点C,于是得到C(-6,0),设直线l的解析式为y=-$\frac{1}{2}$x+b,把C(-6,0)代入y=-$\frac{1}{2}$x+b即可得到结论.
解答 解:(1)∵直线y=-$\frac{1}{2}$x+3与x轴、y轴分别交于A、B两点,
∴A(6,0),B(0,3),
∴OA=6,OB=3,
∵∠AOB=90°,
∴tan∠ABO=$\frac{OA}{OB}$=$\frac{6}{3}$=2;
(2)将点A向左平移12个单位到点C,
∴C(-6,0),
∵直线l过点C且与直线y=-$\frac{1}{2}$x+3平行,
设直线l的解析式为y=-$\frac{1}{2}$x+b,
把C(-6,0)代入y=-$\frac{1}{2}$x+b得0=-$\frac{1}{2}×$(-6)+b,
∴b=-3,
∴直线l的解析式为y=-$\frac{1}{2}$x-3.
点评 本题考查了两直线平行或相交问题,坐标与图形变换-平移,解直角三角形,正确的理解题意是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 对我国初中学生视力状况的调查 | |
| B. | 对“最强大脑”节目收视率的调查 | |
| C. | 对一批节能灯管使用寿命的调查 | |
| D. | 对量子科学通信卫星上某种零部件的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
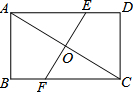 如图,在矩形ABCD中,AD=4,CD=3,对角线AC的垂直平分线分别交AD、BC于点E、F,垂足为O,则EF的长为$\frac{15}{4}$.
如图,在矩形ABCD中,AD=4,CD=3,对角线AC的垂直平分线分别交AD、BC于点E、F,垂足为O,则EF的长为$\frac{15}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
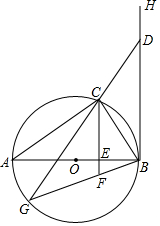 已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4$\sqrt{3}$.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4$\sqrt{3}$.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
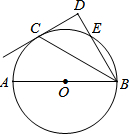 如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.
如图,点C在以AB为直径的⊙O上,BD与过点C的切线垂直于点D,BD与⊙O交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com