
【题目】在平面直角坐标系中,直线 y = x与反比例函数![]() 的图象交于点A(2,m).
的图象交于点A(2,m).

(1)求m和k的值;
(2)点P(xP,yP)是函数![]() 图象上的任意一点,过点P作平行于x轴的直线,交直线y=x于点B.
图象上的任意一点,过点P作平行于x轴的直线,交直线y=x于点B.
①当yP = 4时,求线段BP的长;
②当BP![]() 3时,结合函数图象,直接写出点P 的纵坐标yP的取值范围.
3时,结合函数图象,直接写出点P 的纵坐标yP的取值范围.
【答案】(1)m=2,k=4 ;(2)①BP=3 ; ② yP≥4或0<yP≤1
【解析】
(1)将A点坐标代入直线y = x中求出m的值,确定出A的坐标,将A的坐标代入反比例解析式中求出k的值;
(2)①由题可知点P 和点B的纵坐标都为4,将纵坐标分别代入两个函数解析式得相应横坐标,即可得到点的坐标,求出BP.②根据函数与不等式的关系,即可得到答案.
(1)解:将A(2,m)代入直线 y = x,得m=2,所以A(2,2),
将A(2,2)代入反比例函数![]() ,得:
,得:![]() ,则k=4
,则k=4
综上所述,m=2,k=4.
(2)①解:作图:

当yP = 4时
点P 和点B的纵坐标都为4
当将y=4,代入 ![]() 得x=1,即P点坐标(1,4)
得x=1,即P点坐标(1,4)
当将y=4,代入y=x得x=4,即B点坐标(4,4)
∴BP=3
②由图可知BP![]() 3时,纵坐标yP的范围: yP≥4或0<yP≤1
3时,纵坐标yP的范围: yP≥4或0<yP≤1


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】某班的同学想测量一教楼AB的高度.如图,大楼前有一段斜坡![]() ,已知
,已知![]() 的长为16米,它的坡度
的长为16米,它的坡度![]() .在离
.在离![]() 点45米的
点45米的![]() 处,测得一教楼顶端
处,测得一教楼顶端![]() 的仰角为
的仰角为![]() ,则一教楼
,则一教楼![]() 的高度约( )米(结果精确到0.1米)(参考数据:
的高度约( )米(结果精确到0.1米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
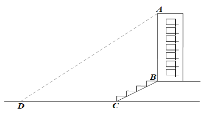
A. 44.1 B. 39.8 C. 36.1 D. 25.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线![]() 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;
(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
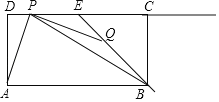
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 与点
与点![]() .
.

(1)求![]() 的长.
的长.
(2)如图2,![]() 点为射线
点为射线![]() 上一动点,连接
上一动点,连接![]() ,线段
,线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交直线
交直线![]() 与点
与点![]() .
.
①若![]() 时,求
时,求![]() 的长:
的长:
②如图3,连接![]() 交直线
交直线![]() 与点
与点![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.

(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(![]() ,2),D(
,2),D(![]() ,
,![]() )中,⊙O的“随心点”是 ;
)中,⊙O的“随心点”是 ;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,∠ABC=45 ,点O是AB的中点,过A、C两点向经过点O的直线作垂线,垂足分别为E、F.
(1)如图①,求证:EF=AE+CF.
(2)如图②,图③,线段EF、AE、CF之间又有怎样的数量关系?请直接写出你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
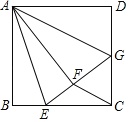
【题目】如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.其中结论正确的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.


(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com