
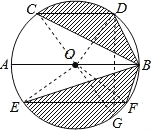
【题目】如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积为_____.

【答案】![]()
【解析】
作直径CG,连接OC、OD、OE、OF、DG、OF,则根据圆周角定理求得DG的长,证明DG=EF,则S扇形ODG=S扇形OEF,然后根据三角形的面积公式证明S△OCD=S△BCD,S△OEF=S△BEF,则S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆,即可求解.
解:作直径CG,连接OC、OD、OE、OF、DG、OF.
∵CG是圆的直径,
∴∠CDG=90°,则DG=![]() =
=![]() =8,
=8,
又∵EF=8,
∴DG=EF,
∴![]() =
=![]() ,
,
∴S扇形ODG=S扇形OEF,
∵AB∥CD∥EF,
∴S△OCD=S△BCD,S△OEF=S△BEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆=![]() π×52=
π×52=![]() π.
π.
故答案是:![]() π.
π.


科目:初中数学 来源: 题型:
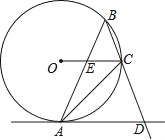
【题目】如图⊙O是△ABC的外接圆,∠ABC=45°,延长BC于D,连接AD,使得AD∥OC,AB交OC于E.
(1)求证:AD与⊙O相切;
(2)若AE=2![]() ,CE=2.求⊙O的半径和AB的长度.
,CE=2.求⊙O的半径和AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2)
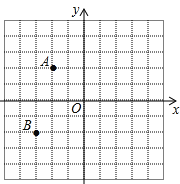
(1)若点D与点A关于y轴对称,则点D的坐标为 .
(2)将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为 .
(3)求A,B,C,D组成的四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形BEFG的边长分别为1和3,点C在边BG上,线段DF、EG交于点M,连接DE、BM,则△DEG的面积为____,BM=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
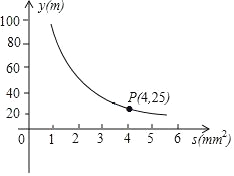
【题目】你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示.
(1)写出y(m)与S(mm2)的函数关系式;
(2)求当面条粗2mm2时,面条的总长度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由甲、乙两个工程队承包某校校园绿化工程,甲、乙两队单独完成这项工程所需时间比是3︰2,两队合做6天可以完成.
(1)求两队单独完成此项工程各需多少天?
(2)此项工程由甲、乙两队合做6天完成任务后,学校付给他们20000元报酬,若
按各自完成的工程量分配这笔钱,问甲、乙两队各得到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小梅、小花四人共同探究代数式x2-4x+5的值的情况,他们作了如下分工:小明负责找值为1时的x值,小亮负责找值为0时的x值,小梅负责找最小值,小花负责找最大值.几分钟后,各自通报探究的结论,其中错误的是( )
A.小明认为只有当x=2时,x2-4x+5的值为1;
B.小亮认为找不到实数x,使x2-4x+5的值为0;
C.小花发现当取大于2的实数时,x2-4x+5的值随x的增大而增大,因此认为没有最大值;
D.小梅发现x2-4x+5的值随x的变化而变化,因此认为没有最小值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 中,AB=AC,过其中一个顶点的直线可以把这个三角形分成另外两个等腰三角形,则∠BAC( )
A. 36°,90°,![]() , 108°B. 36°,72°,
, 108°B. 36°,72°,![]() ,90°
,90°
C. 90°,72°,108°,![]() D. 36°,90°,108°,
D. 36°,90°,108°,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com