
����Ŀ����������Ҫ���������⣮
��1���벹ȫ������ʽ��2x2��4x��0�Ľ⼯�Ĺ��̣�
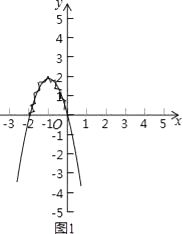
�ٹ��캯��������ͼ���ݲ���ʽ����������κ���y=��2x2��4x���������������ϵ�У�ͼ1���������κ���y=��2x2��4x��ͼ��ֻ����ͼ�ɣ���
����ý�㣬��ʾ���裬��y=0ʱ����÷��̩�2x2��4x=0�Ľ�Ϊ�� �������þ���߱�ʾ������y=��2x2��4xͼ����y��0�IJ��֣�
�۽���ͼ��д���⼯��������ʾͼ�ɵò���ʽ��2x2��4x��0�Ľ⼯Ϊ��2��x��0����������������һԪһ�β���ʽ�⼯�Ĺ��̣���ʽx2��2x+1��4�Ľ⼯��
���𰸡�
��1���⣺��ͼ��ʾ��
��x1=0��x2=��2����3��x��3��x�ܩ�1��
�ۺ���y=x2��2x+1��ͼ���ǣ�
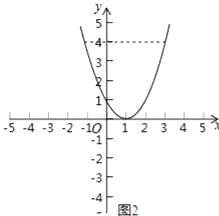
��y=4ʱ��x2��2x+1=4����ã�x1=3��x2=��1��
��ʽ�Ľ⼯�ǣ�x��3��x�ܩ�1��
���������ڷ��̩�2x2��4x=0����2x��x+2��=0��
��ã�x1=0��x2=��2��
�̵Ľ���x1=0��x2=��2��
ͼ����ͼ1��
��������ʽ�ֽⷨ����dz��Ľ⣻�ٻ���y=��2x2��4x��ͼ�۲캯��ͼ���þ���߱�ʾ��y��0�IJ��֡�
�����������x2��2x+1=4�Ľ⣬�ٻ�������y=x2��2x+1��ͼ���ٹ۲캯��ͼ����y��4ʱ�Ա�����ȡֵ��Χ�����Ȼ���y=x2-2x-3���ٹ۲�y��0ʱ�Ա�����ȡֵ��Χ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ�Ķ���
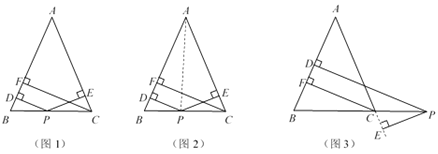
��ͼ1������ABC�У�AB��AC����PΪ��BC�ϵ�����һ�㣬����P��PD��AB��PE��AC������ֱ�ΪD��E������C��CF��AB������ΪF����֤��PD��PE��CF��
СҢ��֤��˼·������ͼ2������AP������ABP����ACP���֮�͵�����ABC���������֤����PD��PE��CF��
���ƹ�������
��ͼ3������P��BC�ӳ�����ʱ�������������䣬��������������������۵ľ���ͷ���������PD��PE��CF��������ϵ����֤����
�����������
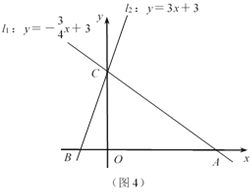
��ͼ4����ƽ��ֱ������ϵ��������ֱ��l1��y����![]() x��3��l2��y��3x��3��l1��l2��x��Ľ���ֱ�ΪA��B��
x��3��l2��y��3x��3��l1��l2��x��Ľ���ֱ�ΪA��B��
(1)����ֱ�ߵĽ���C������Ϊ ��
(2)˵����ABC�ǵ��������Σ�
(3)��l2�ϵ�һ��M��l1�ľ�����1����������Ľ��ۣ����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O�����ߣ�BΪ�е㣬AO���ӳ��߽���O�ڵ�C������BC�������A=30�㣬AB=2 ![]() ����ôAC�ij����ڣ� ��
����ôAC�ij����ڣ� ��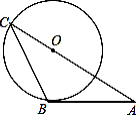
A.4
B.6
C.4 ![]()
D.6 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶һ��С�������赽ˮ���г�����ˮ������һ��ˮ��̯ǰ�����������ۻ�Ա�ĶԻ���
���裺���ۻ�Աͬ־���������Щ�ϴ���.��
�ۻ�Ա�������裬���ϴ���������涼�����ˣ����ǻ�û���ü��������ҽ����������Щ�½���ƻ�����۸�����һ�㣬����ƻ����Ӫ����ֵ����.��
���裺���ã����ǵķ���̬�Ⱥͷ��������Һ����⣬��������ϴ�һ����Ҳ��30ԪǮ��ƻ����.���ؼҺ����ǰ�����εĵ���СƱ��С�ŷ��֣�ÿǧ��ƻ���ĵ��ۼ�����ĵ��۵�1.5����ƻ��������������2.5ǧ��.
С�Ÿ�������ĶԻ��ͷ�Ʊ����������ƻ���ĵ��ۣ���֪�����ƻ���ĵ��۸��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��
��![]()
=![]()
=![]() =
=![]() ��
��
����������⣺
��1���ں�ʽ![]() �У���6��Ϊ______����n����__________��
�У���6��Ϊ______����n����__________��
��2��������͵��뷨��ͨ�����÷�ʽ����������ʽ�еĸ�����ת��Ϊ������֮�ʹ�ó���ĩ��������м����ĺ�Ϊ_______���Ӷ��ﵽ��͵�Ŀ�ģ�
��3���ܴ����������������ķ��̣�
![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����R t��ABC�У���C��90�㣬��BAC�Ľ�ƽ����AD��BC����D��
��1�����ֲ��������ó߹�������AB����һ��OΪԲ�ģ���A��D��������O����AB����һ������ΪE����AC����һ������ΪF����д������������ͼ�ۼ��������ж�ֱ��BC���O��λ�ù�ϵ����˵�����ɡ�
��2������BAC=60�ȣ�CD= ![]() �����߶�BD��BE���ӻ�DE��Χ�ɵ�ͼ�������������������ź�
�����߶�BD��BE���ӻ�DE��Χ�ɵ�ͼ�������������������ź� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��DΪBC����һ�㣬��B=30����DAB=45�㣮��1�����DAC�Ķ�������2����˵����AB=CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������в���ʽ��
��1���ⲻ��ʽ�� �����ѽ⼯�������ϱ�ʾ������
�����ѽ⼯�������ϱ�ʾ������
��2����ʽ��2��3x��7��8�����������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬ ABCD �۵���AE��EF Ϊ�ۺۣ��� C ���� AD ���ϵ� G ���� ���ҵ� B ���� EG �ߵ� H ������ AB=![]() ����BAE=30������ BC �ߵij�Ϊ�� ��
����BAE=30������ BC �ߵij�Ϊ�� ��

A. 3 B. 4 C. 5 D. 6
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com