【题目】已知：正比例函数图像经过点P（3,4）和点Q（6，m）
（1）求正比例函数解析式及点Q的坐标
（2）在x轴上求一点M，使△MPQ的面积等于18
【答案】（1）正比例函数解析式为y=
x，Q（6，8）；（2）M（9，0）或（-9，0）
【解析】
（1）设正比例函数解析式为y=kx，把P坐标代入求出k的值，确定出解析式，再将Q点坐标代入求出m的值即可．
（2）设M点坐标为（t，0）,根据△MPQ的面积=△MOQ的面积-△MOP的面积=18，列出关于t的方程即可
解：（1）设正比例函数解析式为y=kx，
∵正比例函数图像经过点P（3,4）
∴3k=4；∴k=
∴正比例函数解析式为y=x
∵点Q（6，m）在正比例函数图像上，
∴m=
∴Q（6，8）
（2）设M点坐标为（t，0）,
∵△MPQ的面积等于18
∴△MOQ的面积-△MOP的面积=18
∴
（8-4）|t|=18，
∴t=
∴M（9，0）或（-9，0）
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案科目：初中数学 来源： 题型：
【题目】以下说法合理的是（ ）
A. 小明在10次抛图钉的试验中发现3次钉尖朝上，由此他说钉尖朝上的概率是30%
B. 抛掷一枚普通的正六面体骰子，出现6的概率是
的意思是每6次就有1次掷得6
C. 某彩票的中奖机会是2%，那么如果买100张彩票一定会有2张中奖。
D. 在一次课堂进行的试验中，甲、乙两组同学估计硬币落地后，正面朝上的概率分别为0．48和0．51。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，已知三角形的三边长，求这个三角形的面积.
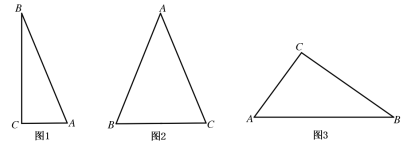
（1）如图1，已知
，
，
，则的面积是______；
（2）如图2，已知
，
，求的面积；
（3）如图3，已知
，，
，求的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】工人师傅做铝合金窗框分下面三个步骤进行：
（1）先截出两对符合规格的铝合金窗料（如图①），使AB=CD，EF=GH；
（2）摆放成如图②的四边形，则这时窗框的形状是______形，根据的数学原理是：_______________________；
（3）将直角尺靠紧窗框的一个角（如图③），调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时（如图④），说明窗框合格，这时窗框是_______形，根据的数学原理是：_____________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC的方向平移，得到△A′B′C′，再将△A′B′C′绕点A′逆时针旋转一定角度后，点B′恰好与点C重合，则平移的距离和旋转角的度数分别为（ ）
A．4，30° B．2，60° C．1，30° D．3，60°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等边三角形，BD是AC边上的高，延长BC至E，使CE=CD，连接DE。
（1）求∠E的度数？
（2）△DBE是什么三角形？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本小题满分10分）已知关于x的方程mx2-(3m－1)x+2m－2=0
（1）求证：无论m取任何实数时，方程恒有实数根.
（2）若关于x的二次函数y= mx2-(3m－1)x+2m－2的图象与x轴两交点间的距离为2时，求抛物线的解析式.
（3）在直角坐标系xoy中，画出（2）中的函数图象，结合图象回答问题：当直线y=x+b与（2）中的函数图象只有两个交点时，求b的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，函数y=
的图象与双曲线y=
（k≠0，x＞0）相交于点A（3，m）和点B．
（1）求双曲线的解析式及点B的坐标；
（2）若点P在y轴上，连接PA，PB，求当PA+PB的值最小时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，
，
，现有动点
从点
出发，沿射线
方向运动，动点
从点
出发，沿射线
方向运动，已知点的速度是
，点的速度是
，它们同时出发，经过________秒，
的面积是面积的一半？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com