
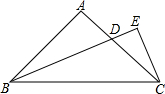
 如图,在△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于点D,CE⊥BD的延长线于点E,求证:BD=2CE.
如图,在△ABC中,∠A=90°,AB=AC,BD平分∠ABC交AC于点D,CE⊥BD的延长线于点E,求证:BD=2CE. 分析 延长BA,CE交于点F,证△ABD≌△ACF,通过角之间的关系,得到BF=BC,又由CE⊥BD,进而可求解.
解答 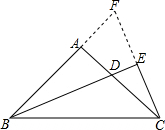 证明:如图所示,延长BA,CE交于点F,
证明:如图所示,延长BA,CE交于点F,
∵∠ABD+∠ADB=90°,∠CDE+∠ACF=90°,
∴∠ABD=∠ACF,
又∵AB=AC,
在Rt△ABD和Rt△ACF中,
$\left\{\begin{array}{l}{∠DBA=∠ACF}\\{AB=AC}\\{∠BAD=∠CAF}\end{array}\right.$,
∴Rt△ABD≌Rt△ACF,
∴BD=CF,
在Rt△FBE和Rt△CBE中,
∵BD平分∠ABC,
∴∠BCF=∠F,
∵∠BEC=90°,
∴∠BEF=∠BEC=90°,
∵BE=BE,
∴Rt△FBE≌Rt△CBE,
∴EF=EC,
∴CF=2CE,
即BD=2CE.
点评 本题考查了全等三角形的判定和性质;熟练掌握全等三角形的性质及判定,会利用一些简单的辅助线辅助解题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:选择题
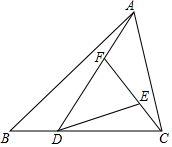 如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )
如图,已知三角形ABC的面积为1,且BD=$\frac{1}{2}$DC,则△DEF的面积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{13}{18}$ | D. | $\frac{8}{27}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 输入 | 执行操作 ×(-$\frac{1}{3}$) | 输出(入) | 执行操作 ÷(-12) | 输出(入) | 执行操作 ÷(-$\frac{1}{4}$) | 输出 |
| 18 | … | a | … | b | … | c |
| d | … | e | … | f | … | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{y}{x}=\frac{xy}{x^2}$ | B. | $\frac{y}{x}=\frac{πy}{πx}$ | C. | $\frac{y}{x}=\frac{yz}{xz}$ | D. | $\frac{y}{x}=\frac{{y({{x^2}+2})}}{{x({{x^2}+2})}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
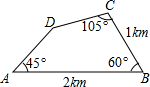 为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )| A. | $\frac{3+\sqrt{6}}{4}$km2 | B. | $\frac{3-\sqrt{6}}{4}$km2 | C. | $\frac{6+\sqrt{3}}{4}$km2 | D. | $\frac{6-\sqrt{3}}{4}$km2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com