练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    若a，b，c为△ABC的三边，且关于x的二次三项式x2+2（a+b+c）x+3（ab+bc+ca）为完全平方式，则△ABC是（ ）
    A．直角三角形
    B．等边三角形
    C．等腰直角三角形
    D．只有两边相等的等腰三角形
    【答案】分析：由x2+2（a+b+c）x+3（ab+bc+ca）为完全平方式可得3（ab+bc+ca）=（a+b+c）2，这样我们通过配方就能得出答案．
    解答：解：由x2+2（a+b+c）x+3（ab+bc+ca）为完全平方式可得3（ab+bc+ca）=（a+b+c）2
    等式两边同时乘2并移项得，a2-2ab+b2+a2-2ac+c2+b2-2bc+c2=0
    ∴（a-b）2+（a-c）2+（b-c）2=0
    解得a=b，a=c，b=c，
    ∴△ABC为等边三角形．
    故选B．
    点评：本题考查完全平方式的知识与三角形的结合，属中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2013•莆田）在Rt△ABC，∠C=90°，D为AB边上一点，点M、N分别在BC、AC边上，且DM⊥DN．作MF⊥AB于点F，NE⊥AB于点E．
    （1）特殊验证：如图1，若AC=BC，且D为AB中点，求证：DM=DN，AE=DF；
    （2）拓展探究：若AC≠BC．
    ①如图2，若D为AB中点，（1）中的两个结论有一个仍成立，请指出并加以证明；
    ②如图3，若BD=kAD，条件中“点M在BC边上”改为“点M在线段CB的延长线上”，其它条件不变，请探究AE与DF的数量关系并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•武侯区一模）已知a、b、c分别是△ABC的∠A、∠B、∠C的对边（c＞b），关于x的方程x2-2（b+c）x+2bc+a2=0有两个相等的实数根，且∠B、∠C满足关系式
    		3
    sin∠B=sin∠C    ，△ABC的外接圆面积为64π．
    （1）求a，b，c的长．
    （2）若D、E、F分别为AB、BC、AC的中点，点P为AB边上的一个动点，PQ∥AC，且交BC于点Q，以PQ为一边向点B的异侧作正三角形PQH，设正三角形PQH与矩形EDAF的公共部分的面积为S，BP的长为
    		3
    x．直接写出S与x之间的关系．
    （3）在（2）的情况下，当x=4
    		3
    时，求S的值．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（福建莆田卷）数学（解析版） 题型：解答题

    在Rt△ABC，∠C=90°，D为AB边上一点，点M、N分别在BC、AC边上，且DM⊥DN．作MF⊥AB于点F，NE⊥AB于点E．

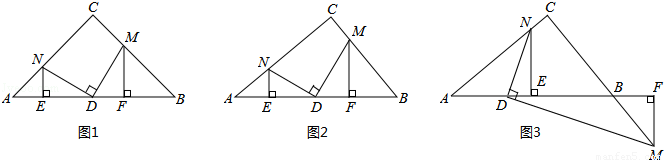
    （1）特殊验证：如图1，若AC=BC，且D为AB中点，求证：DM=DN，AE=DF；

    （2）拓展探究：若AC≠BC．

    ①如图2，若D为AB中点，（1）中的两个结论有一个仍成立，请指出并加以证明；

    ②如图3，若BD=kAD，条件中“点M在BC边上”改为“点M在线段CB的延长线上”，其它条件不变，请探究AE与DF的数量关系并加以证明．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在Rt△ABC，∠C=90°，D为AB边上一点，点M、N分别在BC、AC边上，且DM⊥DN．作MF⊥AB于点F，NE⊥AB于点E．

    （1）特殊验证：如图1，若AC=BC，且D为AB中点，求证：DM=DN，AE=DF；

    （2）拓展探究：若AC≠BC．

    ①如图2，若D为AB中点，（1）中的两个结论有一个仍成立，请指出并加以证明；

    ②如图3，若BD=kAD，条件中“点M在BC边上”改为“点M在线段CB的延长线上”，其它条件不变，请探究AE与DF的数量关系并加以证明．

    查看答案和解析>>

    科目：初中数学 来源：2004年云南省中考数学试卷（解析版） 题型：选择题

    （2004•云南）如图，若△ABC的三边长分别为AB=9，BC=5，CA=6，△ABC的内切圆⊙O切AB、BC、AC于D、E、F，则AF的长为（ ）
    A．5
    B．10
    C．7.5
    D．4

    查看答案和解析>>

    同步练习册答案