
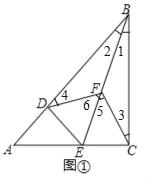
【题目】如图,已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE的中点,连接CF,DF.

(1)如图1,当点D在AB上,点E在AC上时
①证明:△BFC是等腰三角形;
②请判断线段CF,DF的关系?并说明理由;
(2)如图2,将图1中的△ADE绕点A旋转到图2位置时,请判断(1)中②的结论是否仍然成立?并证明你的判断.
【答案】(1)①证明见解析;②结论:CF=DF且CF⊥DF.理由见解析;(2)(1)中的结论仍然成立.理由见解析.
【解析】分析:(1)、根据“直角三角形斜边上的中线等于斜边的一半”可知CF=BF=EF,根据∠CFD=2∠ABC,∠ACB=90°,∠ABC=45°得出∠CFD=90°,从而得出答案;(2)、延长DF至G使FG=DF,连接BG,CG,DC,首先证明△BFG和△EFD全等,然后再证明△BCG和△ACD全等,从而得出GC=DC,∠BCG=∠ACD,∠DCG=∠ACB=90°,最后根据直角三角形斜中线的性质得出答案.
详解:(1)①证明:∵∠BCE=90°.EF=FB,∴CF=BF=EF,∴△BFC是等腰三角形.
②解:结论:CF=DF且CF⊥DF.理由如下:
∵∠ADE=90°,∴∠BDE=90°,又∵∠BCE=90°,点F是BE的中点,∴CF=DF=![]() BE=BF,
BE=BF,
∴∠1=∠3,∠2=∠4,∴∠5=∠1+∠3=2∠1,∠6=∠2+∠4=2∠2,
∴∠CFD=∠5+∠6=2(∠1+∠2)=2∠ABC,
又∵△ABC是等腰直角三角形,且∠ACB=90°,∴∠ABC=45°,∴∠CFD=90°,
∴CF=DF且CF⊥DF.
(2)(1)中的结论仍然成立.理由如下:
如图,延长DF至G使FG=DF,连接BG,CG,DC,∵F是BE的中点,∴BF=EF,
又∵∠BFG=∠EFD,GF=DF,∴△BFG≌△EFD(SAS),∴∠FBG=∠FED,BG=ED,
∴BG∥DE,∵△ADE和△ACB都是等腰直角三角形,
∴DE=DA,∠DAE=∠DEA=45°,AC=BC,∠CAB=∠CBA=45°,
又∵∠CBG=∠EBG﹣∠EBA﹣∠ABC=∠DEF﹣(180°﹣∠AEB﹣∠EAB)﹣45°
=∠DEF﹣180°+∠AEB+∠EAB﹣45°=(∠DEF+∠AEB)+∠EAB﹣225°
=360°﹣∠DEA+∠EAB﹣225°=360°﹣45°+∠EAB﹣225°=90°+∠EAB,
而∠DAC=∠DAE+∠EAB+∠CAB=45°+∠EAB+45°=90°+∠EAB,
∴∠CBG=∠DAC,又∵BG=ED,DE=DA,∴BG=AD,又∵BC=AC,
∴△BCG≌△ACD(SAS),∴GC=DC,∠BCG=∠ACD,
∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°,
∴△DCG是等腰直角三角形,又∵F是DG的中点,∴CF⊥DF且CF=DF.



 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,请根据图中信息,回答下列问题:
![]()
(1)a,b,c三个数中,为正数的数是 ,为负数的数是 ;
(2)将|a|,|b|,|c|三个数用不等号“<”连接起来是 ;
(3)化简:|b﹣a|﹣|b+c|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个实数根为x1,x2(x1<x2),分别以x1,x2为横坐标和纵坐标得到点M(x1,x2),则称点M为该一元二次方程的衍生点.
(1)若方程为x2-2x=0,写出该方程的衍生点M的坐标.
(2)若关于x的一元二次方程x2-(2m+1)x+2m=0(m<0)的衍生点为M,过点M向x轴和y轴作垂线,两条垂线与坐标轴恰好围成一个正方形,求m的值.
(3)是否存在b,c,使得不论k(k≠0)为何值,关于x的方程x2+bx+c=0的衍生点M始终在直线y=kx-2(k-2)的图象上,若有请直接写出b,c的值,若没有说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚,为了了解我市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷包括五个项目:A:健身房运动;B:跳广场舞;C:参加暴走团;D:散布;E:不运动.
以下是根据调查结果绘制的统计图表的一部分.
运动形式 | A | B | C | D | E |
人数 | 12 | 30 | m | 54 | 9 |
请你根据以上信息,回答下列问题:
(1)接受问卷调查的共有 人,图表中的m= ,n= ;
(2)统计图中,A类所对应的扇形圆心角的度数为 ;
(3)根据调查结果,我市市民最喜爱的运动方式是 ,不运动的市民所占的百分比是 ;
(4)我市碧沙岗公园是附近市民喜爱的运动场所之一,每晚都有“暴走团”活动,若最邻近的某社区约有1500人,那么估计一下该社区参加碧沙岗“暴走团”的大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,点E,F分别在边BC,AD上,且AF=CE.

(Ⅰ)如图①,求证四边形AECF是平行四边形;
(Ⅱ)如图②,若∠BAC=90°,且四边形AECF是边长为6的菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD,点A(0,1),点C、D在反比例函数![]() (k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为_____.
(k>0)的图象上,AB与x轴的正半轴相交于点E,若E为AB的中点,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从![]() 地出发,晚上到达
地出发,晚上到达![]() 地,然后返回到出发地
地,然后返回到出发地![]() .约定向东为正方向,当天的航行路程记录如下(单位:千米):
.约定向东为正方向,当天的航行路程记录如下(单位:千米):
14,![]() ,
,![]() ,
,![]() ,13,
,13,![]() ,
,![]() ,
,![]()
(1)请你帮忙确定![]() 地在
地在![]() 地的_________方___________千米处;
地的_________方___________千米处;
(2)救灾过程中,冲锋舟离出发点![]() 最远处有多远?
最远处有多远?
(3)若冲锋舟每千米耗油0.4升,油箱容量为30升,晚上冲锋舟能回到出发地![]() 吗?若能,请说明理由,若不能,求冲锋舟至少还需补充多少升油?
吗?若能,请说明理由,若不能,求冲锋舟至少还需补充多少升油?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com