
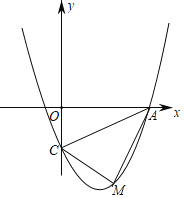
【题目】如图,抛物线经过点A(4,0)、B(﹣2,0)、C(0,﹣4)
(1)求抛物线的解析式;
(2)在抛物线AC段上是否存在点M,使△ACM的面积为3,求出在此时M的坐标,若不存在,说明理由.
【答案】(1)y=![]() ;(2)存在,M1(1,﹣
;(2)存在,M1(1,﹣![]() ),M2(3,﹣
),M2(3,﹣![]() ).
).
【解析】
(1)设交点式为y=a(x﹣4)(x+2),然后把(0,﹣4)代入求出a即可;
(2)设M(a,![]() ),连接OM,则S△ACM=S△OCM+S△OAM﹣S△OAC=3,可得出关于a的方程,解方程即可求出点M的坐标.
),连接OM,则S△ACM=S△OCM+S△OAM﹣S△OAC=3,可得出关于a的方程,解方程即可求出点M的坐标.
解:(1)设抛物线解析式为:y=a(x﹣4)(x+2),
把(0,﹣4)代入得a×(﹣4)×2=﹣4,解得a=![]() ,
,
∴抛物线解析式为:y=![]() ;
;
(2)设M(a,![]() ),连接OM,
),连接OM,

∵S△ACM=S△OCM+S△OAM﹣S△OAC=3,
∴![]() ﹣
﹣![]() =3,
=3,
∴a2﹣4a+3=0,
解得:a1=3,a2=1.
∴M1(1,﹣![]() ),M2(3,﹣
),M2(3,﹣![]() ).
).


科目:初中数学 来源: 题型:
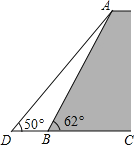
【题目】如图,一堤坝的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
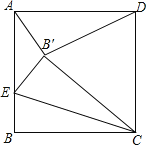
【题目】如图,正方形ABCD中,AB=2,点E是AB上一点,将正方形沿CE折叠,点B落在正方形内一点B'处,若△AB'D为等腰三角形,则BE的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 对角线
对角线![]() 上一动点(
上一动点(![]() 与
与![]() 、
、![]() 不重合),点
不重合),点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
![]() 求证:①
求证:①![]() ;②
;②![]() ;
;
![]() 设
设![]() ,
,![]() 的面积为
的面积为![]() .
.
①求出![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②当![]() 取何值时,
取何值时,![]() 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)画出△ABC关于y 轴对称的△A1B1C1,并写出A1、B1、C1的坐标.
(2)将△ABC向右平移6个单位,画出平移后的△A2B2C2;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.

查看答案和解析>>
科目:初中数学 来源: 题型:
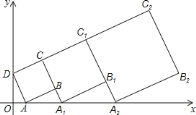
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .延长
.延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,按这样的规律进行下去,第
,按这样的规律进行下去,第![]() 个正方形(正方形
个正方形(正方形![]() 看作第
看作第![]() 个)的面积为( )
个)的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
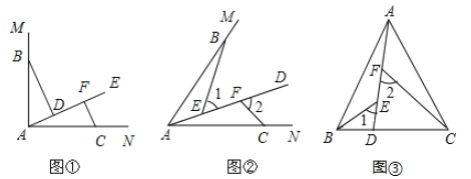
【题目】(1)如图①,![]() ,射线
,射线![]() 在这个角的内部,点
在这个角的内部,点![]() 、
、![]() 分别在
分别在![]() 的边
的边![]() 、
、![]() 上,且
上,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(2)如图②,点![]() 、
、![]() 分别在
分别在![]() 的边
的边![]() 、
、![]() 上,点
上,点![]() 、
、![]() 都在
都在![]() 内部的射线
内部的射线![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角.已知
的外角.已知![]() ,且
,且![]() .求证:
.求证:![]() ;
;
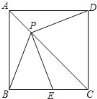
(3)如图③,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .若
.若![]() 的面积为15,求
的面积为15,求![]() 与
与![]() 的面积之和.
的面积之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com