
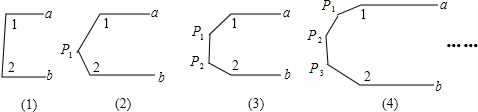
分析 分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°于是得到∠1+∠2=10°,∠1+∠P1+∠2=2×180,∠1+∠P1+∠P2+∠2=3×180°,∠1+∠P1+∠P2+∠P3+∠2=4×180°,根据规律得到结果∠1+∠2+∠P1+…+∠Pn=(n+1)×180°.
解答  解:如图,分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,
解:如图,分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,
∵AB∥CD,
∴AB∥P1E∥P2F∥P3G.
由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°
∴(1)∠1+∠2=180°,(2)∠1+∠P1+∠2=2×180,(3)∠1+∠P1+∠P2+∠2=3×180°,(4)∠1+∠P1+∠P2+∠P3+∠2=4×180°,
∴∠1+∠2+∠P1+…+∠Pn=(n+1)×180°.
故答案为:(n+1)×180.
点评 本题考查的是平行线的性质,根据题意作出辅助线,利用两直线平行,同旁内角互补是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,等边△ABC的边长是4,点P是边AB上任意一点(可与A、B重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB的长为x,PQ的长为y,则y与x的函数关系图象是( )
如图,等边△ABC的边长是4,点P是边AB上任意一点(可与A、B重合),作PD⊥BC于D,作DE⊥AC于E,作EQ⊥AB于Q,设PB的长为x,PQ的长为y,则y与x的函数关系图象是( )| A. | 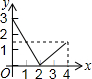 | B. | 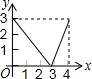 | C. |  | D. | 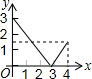 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 中学生最喜欢的电视节目 | |
| B. | 某张试卷上的印刷错误 | |
| C. | 质检部门对各厂家生产的电池使用寿命的调查 | |
| D. | 中学生上网情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com