
| 收地 运地 | C | D | 总计(吨) |
| A | x | 200-x | 200 |
| B | 240-x | x+60 | 300 |
| 总计(吨) | 240 | 260 | 500 |
分析 (1)根据题意之间的数量关系可以直接得出结论;
(2)根据运费=每吨的运费×数量就可以分别表示出yA元,yB元与x之间的数量关系;
(3)首先由B村的荔枝运费不得超过4830元得出不等式,再由两个函数和,根据自变量的取值范围,求得最值.
解答 解:(1)由题意,得
| 收地 运地 | C | D | 总计(吨) |
| A | x | 200-x | 200 |
| B | 240-x | x+60 | 300 |
| 总计(吨) | 240 | 260 | 500 |
点评 本题考查了一次函数的运用,一元一次不等式的运用,总价=单价×数量的运用,解答时求出一次函数的解析式是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠BAC=90°,点E是BC的中点,AD平分∠BAC,BD⊥AD于点D.
如图,Rt△ABC中,∠BAC=90°,点E是BC的中点,AD平分∠BAC,BD⊥AD于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 度数 | 900 | 920 | 950 | 1010 | 1050 | 1100 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,长方形ABCD的边BC∥x轴,若A点的坐标为(-1,2$\sqrt{2}$),C点坐标为(3,-2$\sqrt{2}$).
在平面直角坐标系中,长方形ABCD的边BC∥x轴,若A点的坐标为(-1,2$\sqrt{2}$),C点坐标为(3,-2$\sqrt{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在10×10的小正方形网格中,△ABC的顶点A、B、C在网格点上,P1、P2、P3、P4是其中一个小正方形的四个格点,将△ABC绕A点逆时针旋转90°,再向下平移2个单位,得到△A′B′C′;将△ABC按一定的规律顺次旋转,第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1;第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2;第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3,依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去.
如图,在10×10的小正方形网格中,△ABC的顶点A、B、C在网格点上,P1、P2、P3、P4是其中一个小正方形的四个格点,将△ABC绕A点逆时针旋转90°,再向下平移2个单位,得到△A′B′C′;将△ABC按一定的规律顺次旋转,第一次将△ABC绕点P1逆时针旋转90°得到△A1B1C1;第二次将△A1B1C1绕点P2逆时针旋转90°得到△A2B2C2;第三次将△A2B2C2绕点P3逆时针旋转90°得到△A3B3C3,依次按旋转中心为P1、P2、P3、P4、P1、P2…旋转下去.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
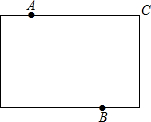 某地拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉P到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请利用尺规作图作出音乐喷泉P的位置.(要求:不写作法,但要保留作图痕迹,必须用铅笔作图).
某地拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉P到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请利用尺规作图作出音乐喷泉P的位置.(要求:不写作法,但要保留作图痕迹,必须用铅笔作图).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com