
【题目】已知![]() .
.

(1)如图1,![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() .试说明:
.试说明:![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() ,那么
,那么![]() (只要直接填上正确结论即可).
(只要直接填上正确结论即可).
【答案】(1)见解析;(2) 49°.
【解析】
(1)首先作FG∥AB,根据直线AB∥CD,可得EF∥CD,据此推得∠ABF+∠CDF=∠BFD即可,再根据BF,DF分别平分∠ABE,∠CDE,推得∠ABF+∠CDF=![]() (∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=
(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=![]() ∠BED;
∠BED;
(2) 连接BD,先求出∠MBD+∠NDB的度数,再求出∠PBM+∠PDN的度数,再利用三角形内角和定理即可解决;
(3)连接BD,先求出∠MBD+∠NDB的度数,再求出∠PBM+∠PDN的度数,再利用三角形内角和定理即可解决.
(1)如图1,作FG∥AB,
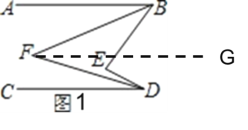
∵直线AB∥CD,
∴FG∥CD,
∴∠ABF=∠BFG,∠CDF=∠GFD,
∴∠ABF+∠CDF=∠BFG+∠GFD=∠BFD,
即∠ABF+∠CDF=∠BFD,
∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
∴∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
(2)连接BD,
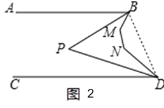
∵∠BMN=133°,∠MND=145°,
∴∠MBD+∠NDB=360°-(133°+145°)=82°,
∵BP、DP分别平分∠ABM、∠NDC,
∴∠PBM=![]() ∠ABM,∠PDN=
∠ABM,∠PDN=![]() ∠CDN,
∠CDN,
∴∠PBM+∠PDN=![]() (180°-82°)=49°,
(180°-82°)=49°,
∴∠BPD=180°-(∠MBD+∠NDB)-(∠PBM+∠PDN)=49°.
故答案为49°.


科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
(1)如图1,当DH=DA时,
①填空:∠HGA= 度;
②若EF∥HG,求∠AHE的度数,并求此时a的最小值;
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
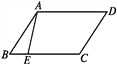
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店老板到体育商场批发篮球、足球、排球共![]() 个,得知该体育商场篮球、足球、排球平均每个
个,得知该体育商场篮球、足球、排球平均每个![]() 元,篮球比排球每个多
元,篮球比排球每个多![]() 元,排球比足球每个少
元,排球比足球每个少![]() 元.
元.
(1) 求出这三种球每个各多少元;
(2) 经决定,该老板批发了这三种球的任意两种共![]() 个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
(3) 该老板打算将每一种球各提价![]() 元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误结论有( );①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在![]() 中,若
中,若![]() ,则
,则![]() 为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)如图①,点D是∠ABC的角平分线BP上一点,连接AD,CD,若∠A与∠C互补,则线段AD与CD有什么数量关系?
(探究)
探究一:如图②,若∠A=90°,则∠C=180°﹣∠A=90°,即AD⊥AB,CD⊥BC,又因为BD平分∠ABC,所以AD=CD,理由是: .
探究二:若∠A≠90°,请借助图①,探究AD与CD的数量关系并说明理由.
[理论]点D是∠ABC的角平分线BP上一点,连接AD,CD,若∠A与∠C互补,则线段AD与CD的数量关系是 .
[拓展]已知:如图③,在△ABC中,AB=AC,∠A=100°,BD平分∠ABC.
求证:BC=AD+BD
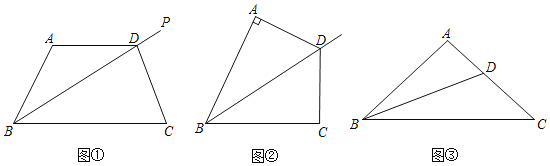
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]()
(1)如图1,若![]() ,则
,则![]() (直接写出结果) .
(直接写出结果) .
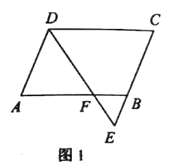
(2)如图2,若![]() 为
为![]() 的点,连接
的点,连接![]() ,求
,求![]() 的值;
的值;
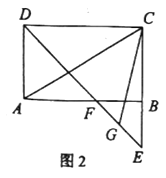
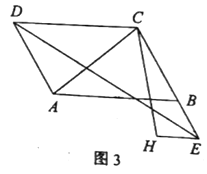
(3)如图3,若![]() 连接
连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各式配成完全平方式:
①x2+6x+______=(x+____)2 ②x2-5x+_____=(x-____)2;
③x2+ x+______=(x+____)2 ④x2-9x+_____=(x-____)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
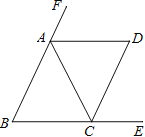
(1)求证:△ABC≌△CDA;
(2)若∠B=60°,求证:四边形ABCD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com