
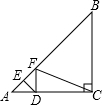
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,点E为AB上一动点,过点E作DE⊥AB交AC于D,将∠A沿 DE翻折,点A落在线段AB上的点F处,当△BCF为等腰三角形时,AE的长为$\frac{2-\sqrt{2}}{2}$或$\frac{1}{2}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,点E为AB上一动点,过点E作DE⊥AB交AC于D,将∠A沿 DE翻折,点A落在线段AB上的点F处,当△BCF为等腰三角形时,AE的长为$\frac{2-\sqrt{2}}{2}$或$\frac{1}{2}$. 分析 分两种情形①BC=BF.②BF=CF分别求解即可.
解答 解:①当BC=BF=$\sqrt{2}$时,
在Rt△ABC中,∵∠ACB=90°,CA=BC=$\sqrt{2}$,
∴∠A=∠B=45°,AB=$\sqrt{2}$BC=2,
∵△DEF是由△DEA翻折得到,
∴AE=AF,△ADF是等腰直角三角形,
∵AF=AB-BF=2-$\sqrt{2}$,
∴AE=$\frac{2-\sqrt{2}}{2}$.
②当FB=FC时,易知AF=BF=CF=1,
∴AE=$\frac{1}{2}$AF=$\frac{1}{2}$.
故答案为$\frac{2-\sqrt{2}}{2}$或$\frac{1}{2}$.
点评 本题考查翻折变换、等腰直角三角形的性质、勾股定理等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,注意不能漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | 1 | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某水库堤坝横断面迎水坡AB的斜面坡度是1:$\sqrt{3}$,堤坝高BC=50m,则迎水坡面AB的长度是( )
如图,某水库堤坝横断面迎水坡AB的斜面坡度是1:$\sqrt{3}$,堤坝高BC=50m,则迎水坡面AB的长度是( )| A. | 100m | B. | 120m | C. | 50$\sqrt{3}$m | D. | 100$\sqrt{3}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知∠ACB=90°,AB=10,AC=8,DE垂直平分AC,垂足为E,DE交AB于D,连结CD,则CD的长为( )
如图,已知∠ACB=90°,AB=10,AC=8,DE垂直平分AC,垂足为E,DE交AB于D,连结CD,则CD的长为( )| A. | 3 | B. | 4 | C. | 4.8 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
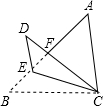 如图,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.
如图,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com