
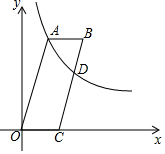
 如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为(8,$\frac{15}{2}$).
如图,四边形OABC是平行四边形,点C在x轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(5,12),且与边BC交于点D.若AB=BD,则点D的坐标为(8,$\frac{15}{2}$). 分析 先根据点A(5,12),求得反比例函数的解析式为y=$\frac{60}{x}$,可设D(m,$\frac{60}{m}$),BC的解析式为y=$\frac{12}{5}$x+b,把D(m,$\frac{60}{m}$)代入,可得b=$\frac{60}{m}$-$\frac{12}{5}$m,进而得到BC的解析式为y=$\frac{12}{5}$x+$\frac{60}{m}$-$\frac{12}{5}$m,据此可得OC=m-$\frac{25}{m}$=AB,过D作DE⊥AB于E,过A作AF⊥OC于F,根据△DEB∽△AFO,可得DB=13-$\frac{65}{m}$,最后根据AB=BD,得到方程m-$\frac{25}{m}$=13-$\frac{65}{m}$,进而求得D的坐标.
解答 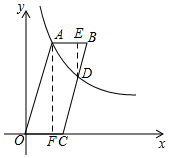 解:∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(5,12),
解:∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(5,12),
∴k=12×5=60,
∴反比例函数的解析式为y=$\frac{60}{x}$,
设D(m,$\frac{60}{m}$),
由题可得OA的解析式为y=$\frac{12}{5}$x,AO∥BC,
∴可设BC的解析式为y=$\frac{12}{5}$x+b,
把D(m,$\frac{60}{m}$)代入,可得$\frac{12}{5}$m+b=$\frac{60}{m}$,
∴b=$\frac{60}{m}$-$\frac{12}{5}$m,
∴BC的解析式为y=$\frac{12}{5}$x+$\frac{60}{m}$-$\frac{12}{5}$m,
令y=0,则x=m-$\frac{25}{m}$,即OC=m-$\frac{25}{m}$,
∴平行四边形ABCO中,AB=m-$\frac{25}{m}$,
如图所示,过D作DE⊥AB于E,过A作AF⊥OC于F,则△DEB∽△AFO,
∴$\frac{DB}{DE}$=$\frac{AO}{AF}$,而AF=12,DE=12-$\frac{60}{m}$,OA=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴DB=13-$\frac{65}{m}$,
∵AB=DB,
∴m-$\frac{25}{m}$=13-$\frac{65}{m}$,
解得m1=5,m2=8,
又∵D在A的右侧,即m>5,
∴m=8,
∴D的坐标为(8,$\frac{15}{2}$).
故答案为:(8,$\frac{15}{2}$).
点评 本题主要考查了反比例函数图象上点的坐标特征以及平行四边形的性质的运用,解决问题的关键是作辅助线构造相似三角形,依据平行四边形的对边相等以及相似三角形的对应边成比例进行计算,解题时注意方程思想的运用.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:选择题
| A. | 三角形的三个内角之比为1:2:3 | B. | 三角形的三边长分别为3,4,5 | ||
| C. | 三角形的三边之比为2:2:3 | D. | 三角形的三边长分别为11,60,61 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
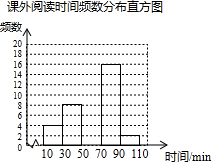 某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.
某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.| 课外阅读时间t | 频数 | 百分比 |
| 10≤t<30 | 4 | 8% |
| 30≤t<50 | 8 | 16% |
| 50≤t<70 | a | 40% |
| 70≤t<90 | 16 | b |
| 90≤t<110 | 2 | 4% |
| 合计 | 50 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数=中位数=平均数 | B. | 中位数<众数<平均数 | ||
| C. | 平均数>中位数>众数 | D. | 平均数<中位数<众数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
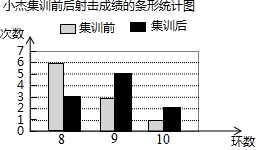 为了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图所示的条形统计图.
为了解射击运动员小杰的集训效果,教练统计了他集训前后的两次测试成绩(每次测试射击10次),制作了如图所示的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>1 | B. | m>0 | C. | m<1 | D. | m<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com