
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
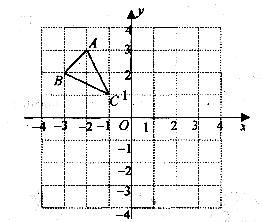
名校联盟冲刺卷系列答案科目:初中数学 来源:不详 题型:解答题

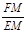 =_______;
=_______;
 角(
角( ),其他条件不变,判断
),其他条件不变,判断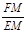 的值是否发生变化,并对你的结论进行证明;
的值是否发生变化,并对你的结论进行证明;
 ,点N在线段OD上,且NO="2." 点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO="2." 点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 同侧,在直线
同侧,在直线 上找一点P,使AP+BP的值最小.
上找一点P,使AP+BP的值最小. 的对称点
的对称点 ,连接
,连接 ,与直线
,与直线 的交点就是所求的点P
的交点就是所求的点P

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
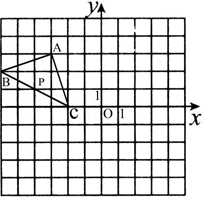
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 位置,且
位置,且 与AC边之间的夹角为30°,那么线段
与AC边之间的夹角为30°,那么线段 的长等于_______。
的长等于_______。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com