
【题目】在平面直角坐标系中,点A、B、C的坐标分别为:A(﹣2,1),B(﹣3,﹣1),C(1,﹣1).若以A,B,C,D为顶点的四边形为平行四边形,那么点D的坐标是_____.
【答案】(﹣6,1)或(2,1)或(0,﹣3)
【解析】
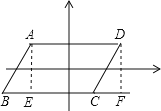
如图,首先易得点D纵坐标为1,然后根据平行四边形性质和全等三角形的性质易得点D横坐标为2;同理易得另外两种情况下的点D的坐标.
解:如图,过点A、D作AE⊥BC、DF⊥BC,垂足分别为E、F,
∵以A,B,C,D为顶点的四边形为平行四边形,
∴AD∥BC,
∵B(﹣3,﹣1)、C(1,﹣1);
∴BC∥x轴∥AD,
∵A(﹣2,1),
∴点D纵坐标为1,
∵ABCD中,AE⊥BC,DF⊥BC,易得△ABE≌△DCF,
∴CF=BE=1,
∴点D横坐标为1+1=2,
∴点D(2,1),
同理可得,当D点在A点左侧时,D点坐标为(﹣6,1);当D点在C点下方时,D点坐标为(0,﹣3);
综上所述,点D坐标为(﹣6,1)或(2,1)或(0,﹣3),
故答案为:(﹣6,1)或(2,1)或(0,﹣3).


科目:初中数学 来源: 题型:
【题目】阅读下列 材料,并解答总题:
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母x+1,可设![]()
则![]()
=![]()
∵对于任意![]() 上述等式成立
上述等式成立
∴![]() ,
,
解得![]() ,
,
∴![]()
这样,分式![]() 就拆分成一个整式
就拆分成一个整式![]() 与一个分式
与一个分式![]() 的和的形式.
的和的形式.
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式为___________;
拆分成一个整式与一个分式(分子为整数)的和的形式为___________;
(2)已知整数![]() 使分式
使分式![]() 的值为整数,则满足条件的整数
的值为整数,则满足条件的整数![]() =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则
y1>y2.其中说法正确的是( )
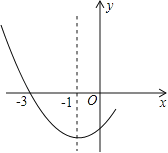
A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题
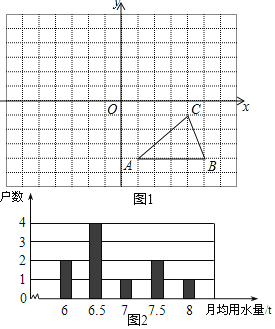
(1)如图1,方格纸中的每个小方格都是边长为1个单位长的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
①作出△ABC关于x轴对称的△A1B1C1;
②如果P点的纵坐标为3,且P点到直线AA的距离为5,请直接写出点P的坐标.
(2)我国是世界上严重缺水的国家之一为了倡导“节约用水,从我做起”,小丽同学在她家所在小区的200住户中,随机调查了10个家庭在2019年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图2
①求这10个样本数据的平均数;
②以上面的样本平均数为依据,自来水公司按2019年该小区户月均用水量下达了2020年的用水计划(超计划要执行阶梯式标准收费)请计算该小区2020年的计划用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线![]() 经过点A(0,3),B(3,0),C(4,3).
经过点A(0,3),B(3,0),C(4,3).
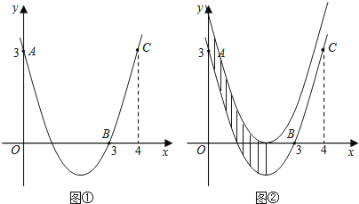
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S(图②中阴影部分).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
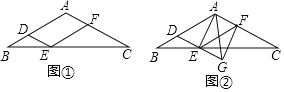
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知卖出的糖果数量x(kg)与售价y(元)的关系如下表:
数量x(kg) | 1 | 2 | 3 | 4 | 5 |
售价y(元) | 2+0.1 | 4+0.2 | 6+0.3 | 8+0.4 | 10+0.5 |
(1)这个表格反映了哪两个变量之间的关系?它们的关系式是什么?
(2)若某顾客付了14.7元,则他购买了多少千克的糖果?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)4(x-1)2=100
(2)x2-2x-15=0
(3)3x2-13x-10=0
(4)3(x-3)2+x(x-3)=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com