Question

20．阅读以下材料：对于三个数a，b，c，用M{a，b，c}表示这三个数的平均数，用min{a，b，c}表示这三个数中最小的数．例如：
M$\left\{{-1，2，3}\right\}=\frac{-1+2+3}{3}=\frac{4}{3}$；min{-1，2，3}=-1；min$\left\{{-1，2，a}\right\}=\left\{\begin{array}{l}a\;\;\;\;\;\;\;\;（a≤-1）\\-1\;\;\;\;\;\;\;（a＞-1）.\end{array}$
解决下列问题：
（1）填空：如果min{2，2x+2，4-2x}=2，则x的取值范围为0≤x≤1．
（2）①如果M{2，x+1，2x}=min{2，x+1，2x}，求x；
②根据①，你发现了结论“如果M{a，b，c}=min{a，b，c}，那么a=b=c（填a，b，c的大小关系）”．
若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}，则x+y=-4．
（3）在同一直角坐标系中作出函数y=x+1，y=$\frac{2}{x}$（x≠0），y=3-x的图象（不需列表描点）．通过观察图象，填空：min$\left\{{x+1，\frac{2}{x}，3-x}\right\}$的最大值为1．

Answer 1

分析 （1）由min{a，b，c}表示这三个数中最小的数可得到x的不等式组，求解即可求得答案；
（2）①由题目所给定义可求得M{2，x+1，2x}=x+1，再同（1）可得到关于x的不等式，可求得x的值；②结合①可得出结论a=b=c，再利用该结论可得到关于x、y的方程组，可求得x、y的值，可求得答案；
（3）可先在坐标系中画出函数图象，再结合题目中所给定义可求得答案．

解答 解：
（1）∵min{2，2x+2，4-2x}=2，
∴$\left\{\begin{array}{l}{2x+2≥2}\\{4-2x≥2}\end{array}\right.$，解得0≤x≤1，
即x的取值范围为0≤x≤1，
故答案为：0≤x≤1；
（2）①∵M{2，x+1，2x}=$\frac{2+x+1+2x}{3}$=x+1=min{2，x+1，2x}，
∴$\left\{\begin{array}{l}{2≥x+1}\\{2x≥x+1}\end{array}\right.$，
∴$\left\{\begin{array}{l}{x≤1}\\{x≥1}\end{array}\right.$，
∴x=1；
②由①可得a=b=c，
证明：∵M{{a，b，c}}=$\frac{a+b+c}{3}$，如果min{a，b，c}=c，则a≥c，b≥c．则有$\frac{a+b+c}{3}$=c，
即a+b-2c=0．
∴（a-c）+（b-c）=0．
又a-c≥0，b-c≥0．
∴a-c=0且b-c=0．
∴a=b=c，
其他情况同理可证，故a=b=c，
∵若M{2x+y+2，x+2y，2x-y}=min{2x+y+2，x+2y，2x-y}，
∴$\left\{\begin{array}{l}{2x+y+2=x+2y}\\{x+2y=2x-y}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$，
∴x+y=-4，
故答案为：a=b=c；-4；
（3）函数图象如图所示．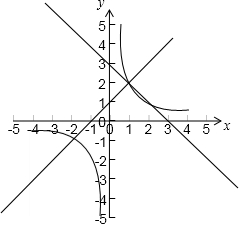

最大值是1．

点评 本题主要考查反比例函数的综合应用，解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的等量关系．