
已知四边形ABCD中,AB∥CD,∠A=∠D=90°,AD=CD=4,AB=7.现有M、N两点同时以相同的速度从A点出发,点M沿A—B—C-D方向前进,点N沿A—D—C-B方向前进,直到两点相遇时停止.设点M前进的路程为 ,△AMN的面积为
,△AMN的面积为 .
.
(1)试确定△AMN存在时,路程 的取值范围.
的取值范围.
(2)请你求出面积S关于路程 的函数.
的函数.
(3)当点M前进的路程为多少时,△AMN的面积最大?最大是多少?
(1)路程 的取值范围
的取值范围 ;
;
(2)当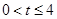 时,
时,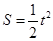 ;
;
当 时,
时, ;
;
当 时,
时, ;
;
当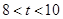 时,
时, ;
;
(3)当点M前进的路程为7时,△AMN的面积最大,最大为14.
解析试题分析:(1)作CE⊥AB于点E,即可得到BE、CE的长,根据勾股定理可以求得CE的长,再根据M、N两点同时以相同的速度从A点出发即可求得结果;
(2)分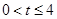 ,
, ,
, ,
,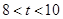 四种情况,根据三角形的面积公式进行分析即可;
四种情况,根据三角形的面积公式进行分析即可;
(3)分别求出(2)中的四种情况下△AMN的面积最大值,再比较即可得到结果.
(1)作CE⊥AB于点E,
则AE=CD=4,CE=AD=4
∵AB=7
∴BE=3
∴
∴AD+CD+BC+AB=20,20÷2=10
∴路程 的取值范围
的取值范围 ;
;
(2)当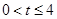 时,
时,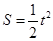 ;
;
当 时,
时, ;
;
当 时,
时, ;
;
当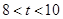 时,
时, ;
;
(3)当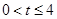 时,
时,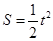 ,最大面积为8;
,最大面积为8;
当 时,
时, ,最大面积为14;
,最大面积为14;
当 时,
时, ,最大面积为14;
,最大面积为14;
当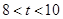 时,
时, ,最大面积为11;
,最大面积为11;
则当点M前进的路程为7时,△AMN的面积最大,最大为14.
考点:动点问题的函数应用
点评:解答本题的关键是读懂题意,根据三角形的面积公式正确列出函数关系式.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2个 | B、3个 | C、4个 | D、6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 年 份 | 2001 | 2002 | 2003 | 2004 | … |
| 财政收入 单位(亿元) |
10 | 10.5 | 12 | 14.5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
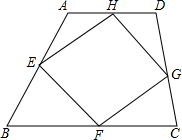 如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com