
抛物线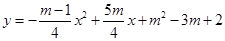 与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上.
与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上.
(1)求点B的坐标;
(2)点P在线段OA上,从点O出发向点A运动,过点P作x轴的垂线,与直线OB交于点E,以PE为边在PE右侧作正方形PEDC(当点P运动时,点C、D也随之运动).
①当正方形PEDC顶点D落在此抛物线上时,求OP的长;
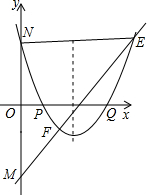
②若点P从点O出发向点A作匀速运动,速度为每秒1个单位,同时线段OA上另一个点Q从点A出发向点O作匀速运动,速度为每秒2个单位(当点Q到达点O时停止运动,点P也停止运动).过Q作x轴的垂线,与直线AB交于点F,在QF的左侧作正方形QFMN(当点Q运动时,点M、N也随之运动).若点P运动到t秒时,两个正方形分别有一条边恰好落在同一条直线上,求此刻t的值.
(1)点B的坐标为(2,4)(2)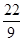
【解析】
试题分析:(1)点B的坐标为(2,4).
(2) ①设OP的长为t,那么PE=2t,ED=2t,点D的坐标为(3t, 2t).当点D落在抛物线上时, .解得
.解得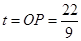 .
.
②当两条边CD与MN在同一条直线上时,点C、N重合,此时6t=10.解得t=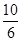 .
.
当两条边CD与QF在同一条直线上时,点C、Q重合,此时5t=10.解得t=2.
当两条边PE与MN在同一条直线上时,点P、N重合,此时4t=10.解得t= .
.
当两条边PE与QF在同一条直线上时,点P、Q重合,此时3t=10.解得t=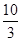 .
.
考点:二次函数的综合题
点评:在解题时要能灵运用二次函数的图象和性质求出二次函数的解析式,利用数形结合思想解题是本题的关键.


科目:初中数学 来源: 题型:
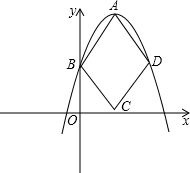 如图,菱形ABCD的三个顶点在二次函数y=ax2-2ax+
如图,菱形ABCD的三个顶点在二次函数y=ax2-2ax+| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| c2 | 4 |
 C所对边的长.
C所对边的长.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
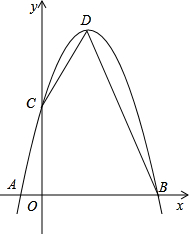 y=-x2+bx+c与x轴的两个交点A、B的横坐标(如下图所示).
y=-x2+bx+c与x轴的两个交点A、B的横坐标(如下图所示).| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4a | b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com