
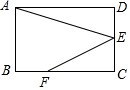
 如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是$\frac{\sqrt{2}}{2}$.
如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是$\frac{\sqrt{2}}{2}$. 分析 接AF,由矩形的性质得出∠B=∠C=90°,CD=AB=2,BC=AD=3,证出AB=FC,BF=CE,由SAS证明△ABF≌△FCE,得出∠BAF=∠CFE,AF=FE,证△AEF是等腰直角三角形,得出∠AEF=45°,即可得出答案.
解答 解:连接AF,如图所示: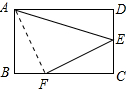
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=2,BC=AD=3,
∵FC=2BF,
∴BF=1,FC=2,
∴AB=FC,
∵E是CD的中点,
∴CE=$\frac{1}{2}$CD=1,
∴BF=CE,
在△ABF和△FCE中,$\left\{\begin{array}{l}{AB=FC}&{\;}\\{∠B=∠C}&{\;}\\{BF=CE}&{\;}\end{array}\right.$,
∴△ABF≌△FCE(SAS),
∴∠BAF=∠CFE,AF=FE,
∵∠BAF+∠AFB=90°,
∴∠CFE+∠AFB=90°,
∴∠AFE=180°-90°=90°,
∴△AEF是等腰直角三角形,
∴∠AEF=45°,
∴cos∠AEF=$\frac{\sqrt{2}}{2}$;
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、三角函数等知识;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| 成绩 | 68 | 67 | 69.5 | 70 | 69 |
| 人数 | 2 | 1 | 2 | 3 | 4 |
| A. | 69,69.5 | B. | 70,69 | C. | 69,69 | D. | 69,70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
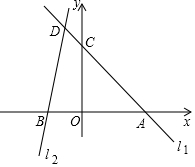 如图,在平面直角坐标系xOy中,直线l1:y=-x+a与x轴交于点A(4,0),与y轴交于点C,直线l2与l1相交于点D(-1,n),与x轴相交于点B(-2,0)
如图,在平面直角坐标系xOy中,直线l1:y=-x+a与x轴交于点A(4,0),与y轴交于点C,直线l2与l1相交于点D(-1,n),与x轴相交于点B(-2,0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
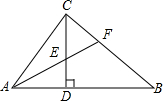 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “经过有交通信号的路口,遇到红灯,”是必然事件 | |
| B. | 已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次 | |
| C. | 处于中间位置的数一定是中位数 | |
| D. | 方差越大数据的波动越大,方差越小数据的波动越小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
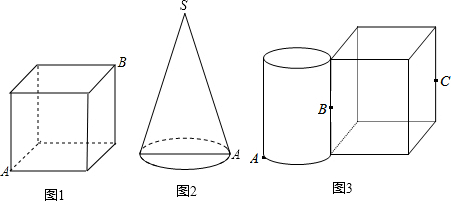
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com