
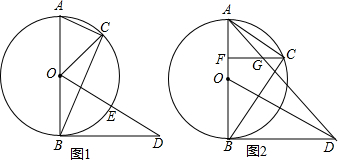
分析 (1)由AB是⊙O的直径,根据直径所对的圆周角为直角得到∠BCA=90°,则∠ABC+∠BAC=90°,而∠CBD=∠BA,得到∠ABC+∠CBD=90°,即OB⊥BD,根据切线的判定定理即可得到BD为⊙O的切线;
(2)连接CE、BE,根据直角三角形斜边上的中线等于斜边的一半得到BE=OE=ED,则△OBE为等边三角形,于是∠BOE=60°,又因为AC∥OD,则∠OAC=60°,AC=OA=OE,即有AC∥OE且AC=OE,可得到四边形OACE是平行四边形,加上OA=OE,即可得到四边形OACE是菱形;
(3)由CF⊥AB得到∠AFC=∠OBD=90°,而AC∥OD,则∠CAF=∠DOB,根据相似三角形的判定易得Rt△AFC∽Rt△OBD,则有$\frac{FC}{BD}$=$\frac{AF}{OB}$,即FC=$\frac{BD•AF}{OB}$,再由FG∥BD易证得△AFG∽△ABD,则$\frac{FG}{BD}$=$\frac{AF}{AB}$,即FG=$\frac{BD•AF}{AB}$,然后求FC与FG的比即可一个定值.
解答 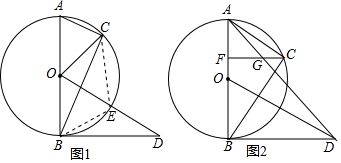 (1)证明:如图1,∵AB是⊙O的直径,
(1)证明:如图1,∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠ABC+∠BAC=90°,
又∵∠CBD=∠BA,
∴∠ABC+∠CBD=90°,
∴∠ABD=90°,
∴OB⊥BD,
∴BD为⊙O的切线;
(2)证明:连接CE、BE,如图1,
∵OE=ED,∠OBD=90°,
∴BE=OE=ED,
∴△OBE为等边三角形,
∴∠BOE=60°,
又∵AC∥OD,
∴∠OAC=60°,
又∵OA=OC,
∴AC=OA=OE,
∴AC∥OE且AC=OE,
∴四边形OACE是平行四边形,
而OA=OE,
∴四边形OACE是菱形;
(3)解:如图2,∵CF⊥AB,
∴∠AFC=∠OBD=90°,
而AC∥OD,
∴∠CAF=∠DOB,
∴Rt△AFC∽Rt△OBD,
∴$\frac{FC}{BD}$=$\frac{AF}{OB}$,即FC=$\frac{BD•AF}{OB}$,
又∵FG∥BD,
∴△AFG∽△ABD,
∴$\frac{FG}{BD}$=$\frac{AF}{AB}$,即FG=$\frac{BD•AF}{AB}$,
∴$\frac{FC}{FG}$=$\frac{AB}{OB}$=2,
∴$\frac{FG}{FC}$=$\frac{1}{2}$.
点评 本题考查了圆的综合题,熟练掌握菱形的判定方法,相似三角形的判定与性质,切线的判定与性质,圆周角定理等知识点,属于中档题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:解答题
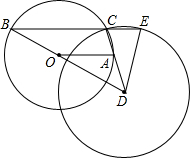 如图,在⊙O中,半径OA长为1,弦BC∥OA,射线BO,射线CA交于点D,以点D为圆心,CD为半径的⊙D交BC延长线于点E.
如图,在⊙O中,半径OA长为1,弦BC∥OA,射线BO,射线CA交于点D,以点D为圆心,CD为半径的⊙D交BC延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=$\frac{2}{3}$
如图,第一象限内的点A、B在反比例函数的图象上,点C在y轴上,BC∥x轴,点A的坐标为(2,4),且tan∠ACB=$\frac{2}{3}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
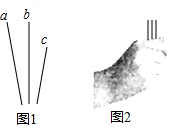 甲、乙、丙三人用三根完全相同的吸管玩游戏,将其中一根剪去一段(如图1所示),甲把三根吸管按如图2所示的方式拿在手中,使露出的部分完全相同,乙先从中抽取一根不放回,丙再从中抽取一根.
甲、乙、丙三人用三根完全相同的吸管玩游戏,将其中一根剪去一段(如图1所示),甲把三根吸管按如图2所示的方式拿在手中,使露出的部分完全相同,乙先从中抽取一根不放回,丙再从中抽取一根.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
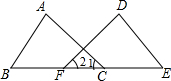 在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.
在数学实践课上,老师在黑板上画出如图的图形,(其中点B,F,C,E在同一条直线上).并写出四个条件:①AB=DE,②∠1=∠2.③BF=EC,④∠B=∠E,交流中老师让同学们从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
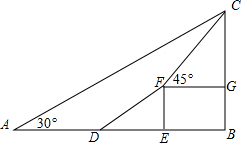 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com